广度优先搜索策略流程（广度优先搜索一般使用什么结构）



回顾 动态规划/(深度优先搜索)/回溯 算法框架

借用二叉树来回顾一下之前学习的 动态规划/(深度优先搜索)/回溯 三种框架：

动态规划框架：

动态规划的本质是将问题分解为多个子问题，找出最优子结构，得出状态转移方程，最后递推出结果。

重叠子问题、最优子结构、状态转移方程 动态规划三要素

(深度优先搜索) 与回溯框架：

• 动态规划属于分解问题的思路，着重点在于每棵子树。
• 算法属于遍历的思路，着重点在于每个节点。
• 回溯算法属于遍历的思路，着重点在于每个树枝。

(广度优先搜索) 算法详解

的核心思想：把一些问题抽象成图，从一个点开始，向四周扩散。 算法一般都会借助队列来遍历图中的所有节点，每遍历到一个新节点，就把与这个节点相连的其他结点加入到队列之中。 算法就是典型的例子。

与 的核心区别在于：找到的路径一定是最短的，但代价就是空间复杂度可能比大很多，从后文的代码框架就很容易看出来了。

算法框架

在介绍框架之前，我们先了解一下算法使用最多的场景，问题的本质就是让你在一个图中找到【start】到终点【target】的最短路径，这个例子听起来枯燥，但其实BFS算法都在干这个事 ，把这个本质弄清楚了，解决经过包装的各种问题才能得心应手嘛。

这个广义的描述可以有各种变体:

• 比如走迷宫，有的格子是围墙，那么从起点到终点的最短距离是多少？如果有的格子会有传送门【实施瞬间传送】呢，最短距离又是多少？
• 再比如说两个单词，要求你通过某些替换，每次替换可以增加、删除或替换一个字符，最少要替换几次呢？（这个在动态规划系列里提到过，表示 转换到所需要的最少操作数）
• 再比如连连看游戏，两个方块消除的条件不仅是图案相同，还得保证两个方块之间的最短连线不能超过两个拐点。玩连连的时候，游戏是如何判断最短连线不超过两个拐点的呢？

变体有很多，但本质就是在一个【图】中，找【start】到【target】的最短路径罢了，只是加了一些限制条件。

框架：

队列 为的核心数据结构，泛指当前节点的所有邻接节点，如果这个图我们用邻接表的形式存储的话，其实就是节点对应的邻接链表，类似的在二维数组中，上下左右四面的位置就是相邻节点，也就是邻接节点。的主要作用是为了防止走回头路，已经遍历过的节点就不要再遍历了，这对于大部分可回头的问题是必须的，但是对于二叉树这种（没有子节点指向父节点的指针）是不需要的。

二叉树的最小高度()

我们通过 判断二叉树的最小高度 这道题来实践一下框架。

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

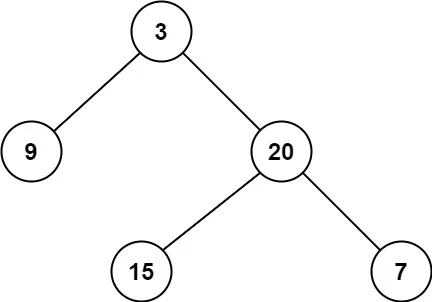
 输入：root = [3,9,20,null,null,15,7]  输出：2

示例 2：

 输入：root = [2,null,3,null,4,null,5,null,6]  输出：5

提示：

• 树中节点数的范围在 内

怎么套框架呢，简单分析后不难发现，这道题的根节点 和 最靠近根节点的叶子节点 就是框架里的【start】与【target】。

 if(cur.left == null && cur.right == null){      //一检测到叶子节点，立马结束      做出相应操作并结束程序，返回结果  }

现在我们只要对框架稍加改造，即可得出结果：

这里注意循环与的配合，循环控制一层一层往下走，循环利用变量从左到右遍历每一层二叉树节点：

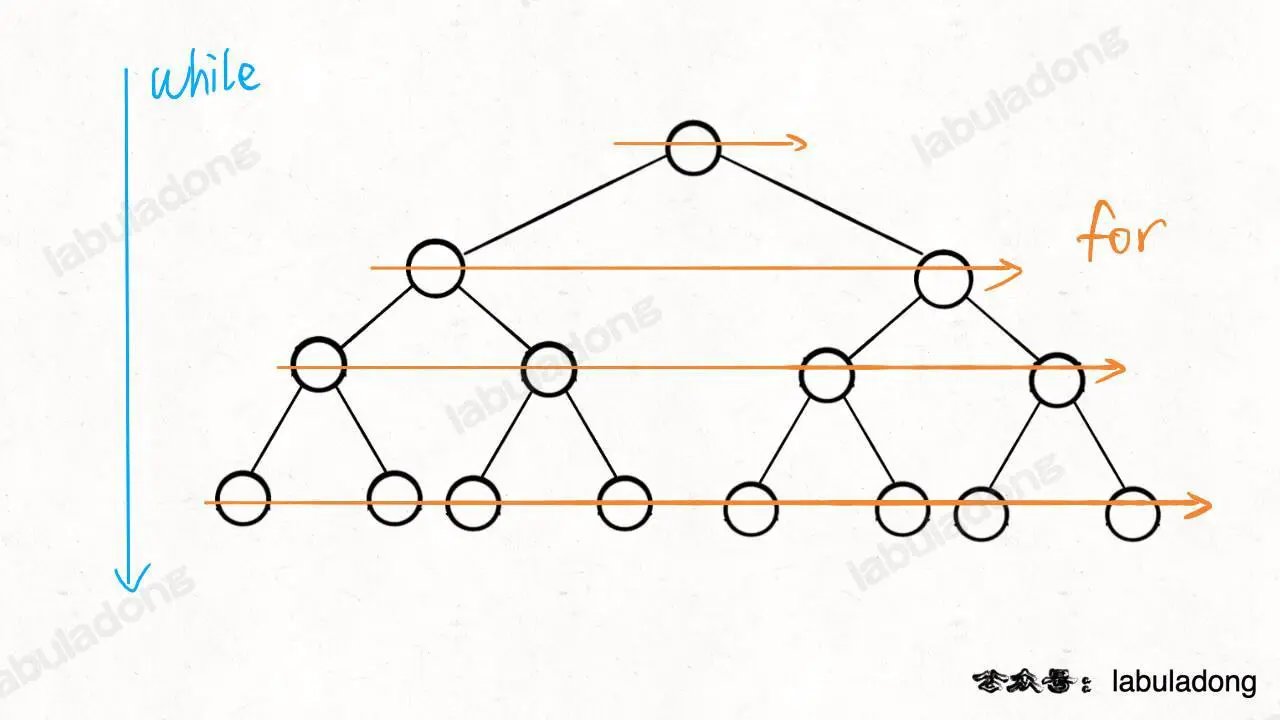
这一点非常重要，这个形式在问题中非常常见，但是在 Dijkstra 算法模板框架 中我们修改了这种代码模式，读完并理解本文后你可以去看看 算法是如何演变成 Dijkstra 算法在加权图中寻找最短路径的。

话说回来，二叉树本身是很简单的数据结构，我想上述代码你应该可以理解的，其实其他复杂问题都是这个框架的变形，再探讨复杂问题之前，我们解答两个问题：

1. 为什么可以找到最短路径，而不行？

首先，看的逻辑，每增加一步，队列中的所有节点都往前迈一步(队列中存的是一层一层的节点)，这保证了第一次到达【target】时的步数是最小的。！！！只是找到了最短路径的长度（从【start】到【target】的最少步数而已）。

如果想找到最短路径的整个路径，即最短路径经过了哪些节点，需要从【target】开始回溯，拿这个【求二叉树的最小深度】举例，我们从终点【target】开始回溯，依着父节点找，一直找到【start】，这条路径就是我们要找的最短路径。

其实也能找到最短路径，只是需要遍历所有的分支，遍历完才能得出最短的路径，而且是依靠递归堆栈来记录走过的路径，这些缺点大大增加了时间复杂度，而借助队列一次实行【齐头并进】，不用遍历完树的所有节点就可找到最短距离。

形象地说，是线，时面，单打独斗，一个节点就往深处走，是集体行动，一层遍历完了之后再进入下一层。

1. 为什么可以找到最短路径，而不行？

虽然可以找到最短距离，但是空间复杂度较大，而所需要的空间复杂度就比较小。

还是拿刚刚的【二叉树最小深度】举例，在最坏情况下，的空间复杂度为最后一层的节点个数，也就是N/2,用Big O 表示的话也就是

O(N),而的空间复杂度也就是递归堆栈所占空间，最坏情况下为O(logN)。

一般来说，一般在寻找最短路径的时候用，其他时候还是用

打开转盘锁

你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字： 。每个拨轮可以自由旋转：例如把 变为 ， 变为 。每次旋转都只能旋转一个拨轮的一位数字。

锁的初始数字为 ，一个代表四个拨轮的数字的字符串。

列表 包含了一组死亡数字，一旦拨轮的数字和列表里的任何一个元素相同，这个锁将会被永久锁定，无法再被旋转。

字符串 代表可以解锁的数字，你需要给出解锁需要的最小旋转次数，如果无论如何不能解锁，返回 。

示例 1:

 输入：deadends = ["0201","0101","0102","1212","2002"], target = "0202"  输出：6  解释：  可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。  注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是不能解锁的，  因为当拨动到 "0102" 时这个锁就会被锁定。

示例 2:

 输入: deadends = ["8888"], target = "0009"  输出：1  解释：把最后一位反向旋转一次即可 "0000" -> "0009"。

示例 3:

 输入: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888"  输出：-1  解释：无法旋转到目标数字且不被锁定。

提示：

• 不在 之中
• 和 仅由若干位数字组成

这道题的密码锁和我们行李箱上的密码锁很类似，如果没有限制的话，我们直接向着密码拨动就行了【第一个位置的数字转换成密码对应位置的数字需要几步 + ... + 最后一个位置的数字转换成密码对应位置的数字需要几步】。

但是现在有了这个限制条件，也就是说不能直接拨过去，可能需要绕一段路，这又该如何计算最少步数【最短距离】呢？

第一步，我们不管与限制条件，就思考一个问题，该怎么设计一个算法穷举所有可能的密码组合？

穷举呗，再贴合题目一点，如果只转一下锁，有多少种可能？很显然，有八种。四个位置，每个位置可以向上转，也可以向下转，总共八种可能。

比如从初始密码状态‘0000’开始，经过一次转锁操作，可以转成‘1000’,’9000’,’0100’,’0900’...等八种密码状态，再以这八种密码状态为基础，每个状态又可以延伸为另外八种状态。

仔细想想，这个问题就可以抽象为图的问题，每个节点有八个邻接节点，又让你求最短距离，这不就是典型的框架吗，我们先写一个适应这个问题的简陋的【先不考虑限制条件和】的框架：

这段代码可以遍历所有密码组合，但是仍然不能解决问题，有以下问题还没解决：

1. 会走回头路，比如说我们从‘0000’拨到‘1000’,但是从队列中拿出‘1000’时，可能还会拨出‘0000’，这样的话会产生死循环，我们需要建立一个集合。
2. 没有终止要求，按照要求，遍历到【target】时就要结束遍历并返回拨动的次数。
3. 没有对的处理，按道理这些【死亡密码】是不能出现的，也就是说你遇到这些密码时需要跳过。

只要稍作修改就可得出最终代码：

版权声明：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符，请将相关资料发送至xkadmin@xkablog.com进行投诉反馈，一经查实，立即处理！

转载请注明出处，原文链接：https://www.xkablog.com/bcyy/13207.html