今天继续介绍图论基础知识。上期内容可点击这篇文章陈关荣丨图论基础(上)。
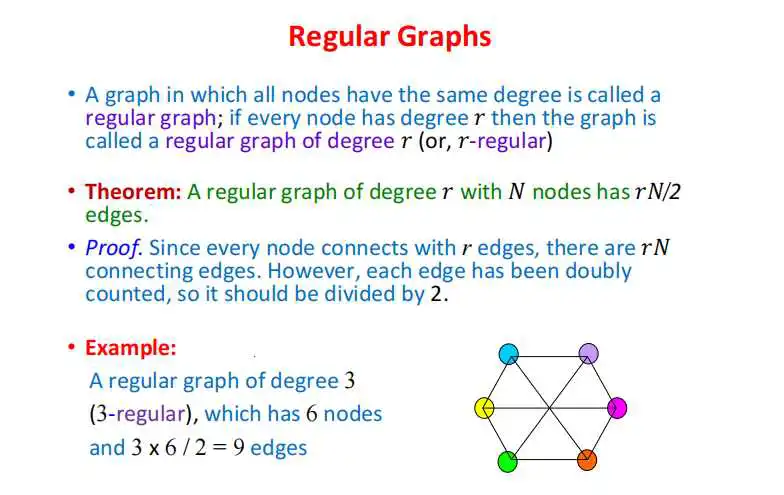
图论中有个概念叫做正则图regular graph。
正则图是什么呢?就是所有节点的度都是一样的图。例如大家的度是2或者大家的度是3等等,这样的图就比较规则了。大家的度是一样的,而且度数等于r的话,就称为r-正则图。上图的例子中我就写了3-正则,因为大家的度是3。那么,有了定义很快就有一些结果。比如r-正则图有N个节点的话,那么它有rN/2条边。因为有N个节点,而每个节点呢,它的度是r,它就跟r条边连在一起。我有三条边,你有三条边,那么就是3乘以2等于6。有N个人的话,r乘以N,总共就有rN条边。但是计算重复了,因为算我的时候算了你,算你的时候又算了我,所以要除以2,结果就出来了。
再来看正则图的特征根
。它们的分布在某种意义上有对称性,因为节点的度都一样。特征根我用μ来表示,区别一下λ,那是拉普拉斯矩阵的特征根。假设一幅r-正则图有N个特征根。它们的排列是有序的,而且下界大于等于-r。比如说每个节点都有度为3的话,这个下界是-3,不会再小了。上界3呢,它不一定能达到,而且这里实际上它永远达不到。如果节点的度都是3的话,那么最大的特征根是小于3的。这就是一个结果,或者说一条定理。还有呢,如果一幅正则图恰好又是二分图,那么当且仅当上面的排列变成了下面的排列。就是说,μ2绝对是大于μ1的,而上面的是大于等于,有可能相等,但下面这里是绝不会相等的。两式右端的上界还是一样的,而且不能达到。
这里是它的定义。定义留给你以后看,现在可以不看,我们来看一个例子你就明白了。
我们来看上图左上角这个例子。我要找它的线图,怎么找?两个步骤:首先,从左上角的图出发到右上角的图。如果节点1跟节点4相连,你这里做个记号,你就写1,4。这是我的记号。你可以用你的记号,一上一下也行。因为它们两个相连,那么1跟3相连,就写下来;1跟2相连,也写下来,等等。全部写完了以后,就拐到左下角的图。刚才写的,如果我有1。你也有1,我们就连起来。另外一个数字不同你不要管,肯定是不同的对吧。只要有共同的,就画一条绿色虚线把它们连接起来。全部走一遍,连好了,不重复不遗漏。连好以后就把绿色虚线改画成黑色实线,这个是你要保留的。原来的连线就全部去掉。还有,原来的节点也全部去掉。那么你就得到右下角这幅图。这幅图绿颜色的那些小块,你重新给它们编号,比如说叫a、b、c等,也是可以的。我保留下来是因为它是从左下角的图得来的,方便你辨识。最后吧,你就有了一幅新的图,这幅图就是原图相应的线图。线图就等于把原来的点换成边了,把原来的边换成点了,可以这么理解,两者有这样置换的关系。当然这只是粗略地去理解,不是一一对应。这个线图在应用上会有些用处。大家可以想象出来的,点和边的位置互换,会带来某些新用途。
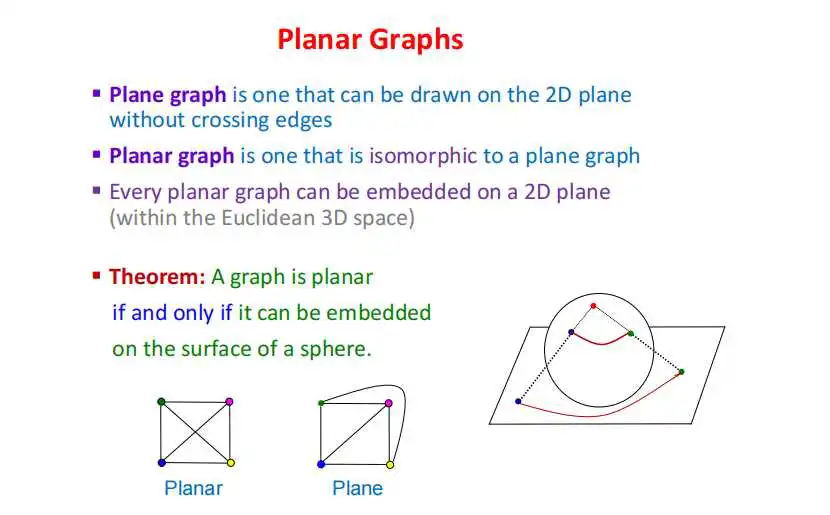
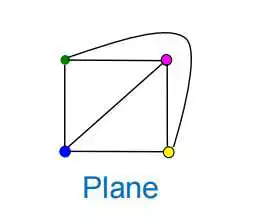
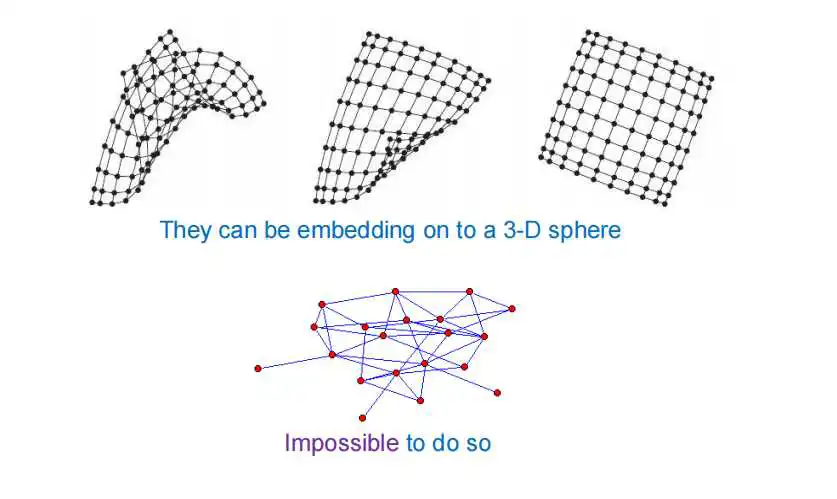
平面图分两种。比如说下面图一,一看就是没有交叉点的。眼睛看上去没有交叉,这个直接就是Plane平面图了。
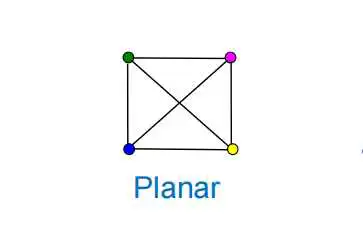
图二看上去它有交叉,但本质上它没有交叉,因为你可以把对角线拉出来,它就变成了图一。因此是Planar,即可平面化的图。它俩英文上有点不一样。有些图需要稍微操作一下才能看得出来它是不是平面图。上面两个平面图是同构的。有个准则,说它是不是平面图,那你就看能不能把它铺在球面上。如果你能把它铺上去的话,那它是平面图,或者说是可以平面化的图,投影到平面上看它就是两种平面图之一。
上面第一排三个图都是,因为你可以把它们铺在球面上没有问题。但是,不是所有图都可以这么做,不然这个概念就没有意义了。第二排这个,你无法把它铺在球面上。你说我把一个球从中间塞进去,不行的,它没有中间空洞的结构让你塞。因此,你不能把它铺在球面上的就是非平面图了。这种图当然有很多。
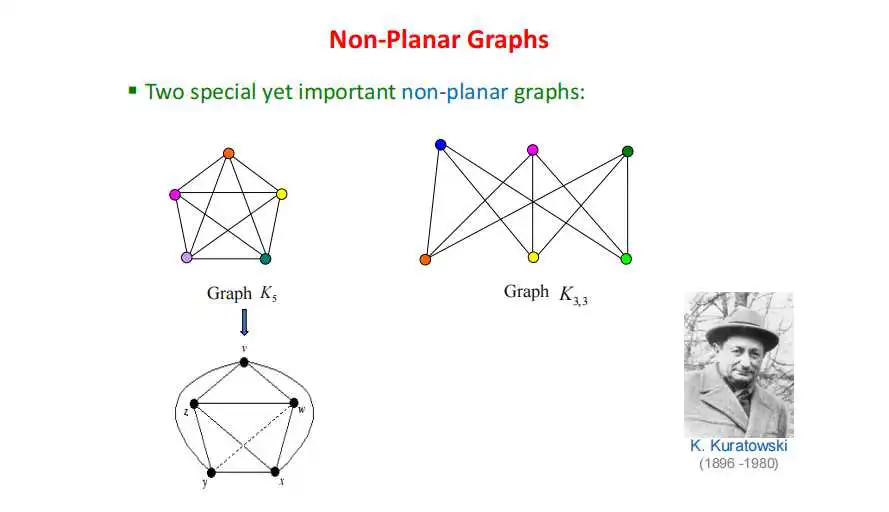
当图或者网络复杂起来,乱七八糟的连接会有很多形式。其中有两幅图特别重要,是波兰数学家(K.Kuratowski)发现的。下图这两幅是很有用的非平面图。
后人用他的名字K命名了左图为k5,右图为k33,其中k33是二分图。这两个都是非平面图。比如说你把k5演变成左下图后,里面两条边你就没有办法再拉出去,连边在平面上总是有交叉的。交叉点不是节点,只是眼睛看上去,你看得出来有交叉点。那么有交叉点再投影的话,它还是有交叉点的,再做投影也没用。K33就更不行了。
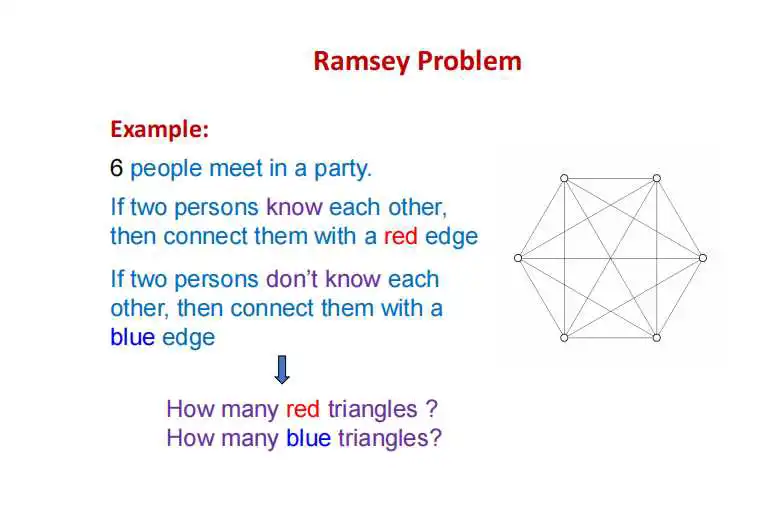
下面你会看到这两个图真的有用。这之前我们先来看另一个有趣的例子,本质上与平面图有关。这个应用例子挺有趣。Ramsey也是个数学家,他说如果你有超过六个人去参加一个聚会,party,比如说60个、101个、1万个,都可以。他说,你去参加聚会的人群里面,我总能找到三个他们是互相认识的,或者总能找到三个他们是互相不认识的,这两种情况总有一种会发生。怎么去验证这个判断呢?他说,如果两个人互相认识的话我把他们的连线标成红色;如果他们互相不认识的话,我把他们之间的连线标成蓝色。下面视频对他的证明作进一步解释。
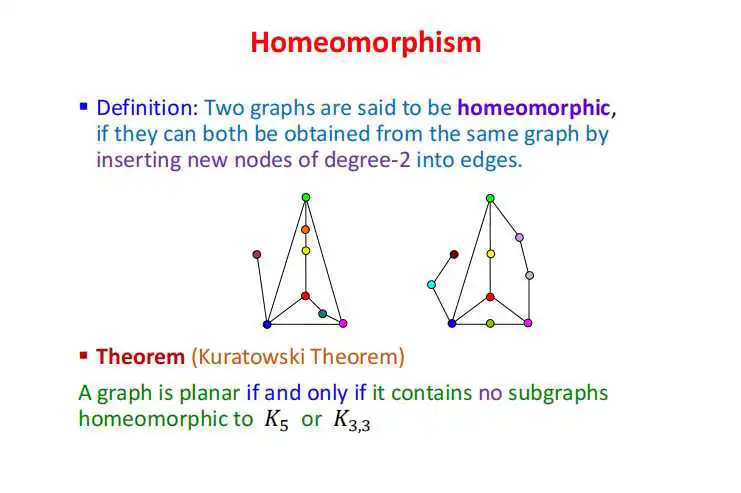
下面这个概念也是蛮重要的,在应用上非常重要,叫做同胚homeomorphism。同胚是什么概念呢?它用来刻画,一幅图有时候某种节点多一些,实际上是无所谓的,影响不大的,不影响它的基本结构。
比如说,上图左边大三角形的右边中间没有节点,我现在加上两个节点,像右图那样。新增节点的度都是2。你先不看别的,把它跟原图相比。它们不同构了,右边的多了两个节点。但其实影响不大。为什么呢?比如说你开车,你中间经过两道桥,我没有过桥,这有啥关系?或者说你不需要交费,我经过了两个收费站。但是我俩都从红点开车到了绿点。不能说它们没有区别,但是在很多应用上来说,这种不同关系不大,不重要,甚至是无所谓的。像我发信号给你,你收到了,中间有没有通过这两个接口有啥关系?你反正收到我给你发的信号了。从这个意义上,引进了同胚这个概念,因为它们并不同构。
我们往下看,还有一些有趣的概念和应用。下面的视频作个简单介绍,用到了K5和K33。
这里,马上又有一些结果了。如果所有的节点的度都比2大的话,那么不管你网络多大、多复杂,里面一定有环路。这个你怎么去证明?
我说明一下就好了。你从某个节点v0出发走到另外一个节点v1。因为这个节点它的度大于2,所以你还有一条路往外走。到了v2,它的度也是大于2的,你还可以往外走。就这样一直走。但只有有限个节点,你最后还是要走回来的,回到前面的某个v。你一回到某个节点,不就形成一条环路了吗?这样,结论就证明了。
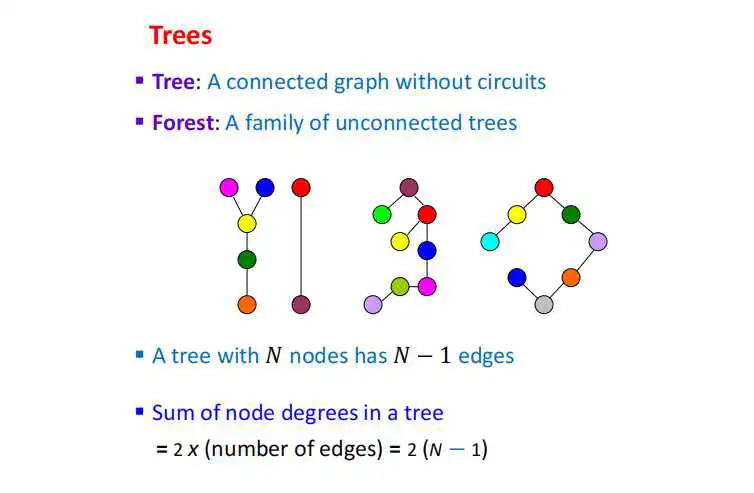
下一个概念是树,比较好理解。树有N个节点和N-1条连边。这刚好就是一棵连通的树。边多了就有环路,少了它就断裂。它们有时候可以排成一条链,但也不见得可以排成一条链。对于树来说,它所有节点度的总和一定是等于2(N-1)。之前讲过,你数一下有多少条边,再乘上2就是了。树非常有用,比如工作分配和数字编码等。树有一些等价的结果或者说特性。它是一棵树当且仅当它有N-1条边并且没有环路、当且仅当它有N-1条边并且是连通的,等等。我不一一列出了,还可以多写几个。
上面所有这些说法都是同一回事,就是说,它是一棵树。
特别有趣的是分形树。分形树有很多很特别很漂亮的特性,这里不详细说了。比如,你可以算一下这里展示的特征。树看上去简单,但是放在分形里面,它非常漂亮。它有一定的规律,既简单又不简单。因为有一定规律,你总能写出一些公式来。
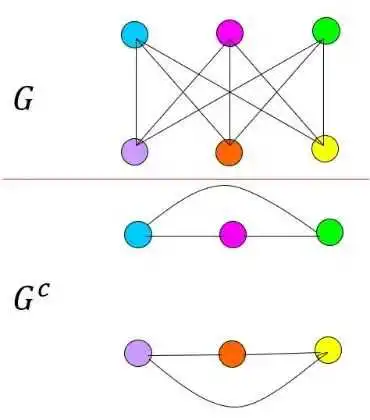
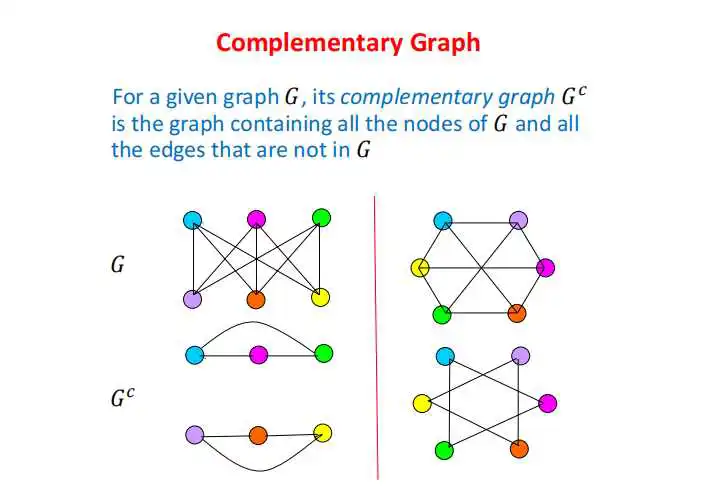
下面还有一个很重要的概念,叫做补图。这里上下两幅图是互为补充的。我给你上面这幅图G,那么下面的Gc就是它的补图。
首先,大家都有相同的节点,这不能变,也不能改。第二呢?你有连线的地方,我没有,比如说你这里有连线,我下面就没有;你没有连线的地方呢,我有。刚好反过来,那么我就是你的补图。反过来说,你也是我的补图。我们两幅互补的图放在一起,节点重叠在一起,这样就得到一幅全连接的图。这个是主要特征,当然还有别的一些特征。后面我讲同步的时候会告诉你,补图非常有用,可以帮助你去判别一个网络的同步能力是不是比另一个网络要好。
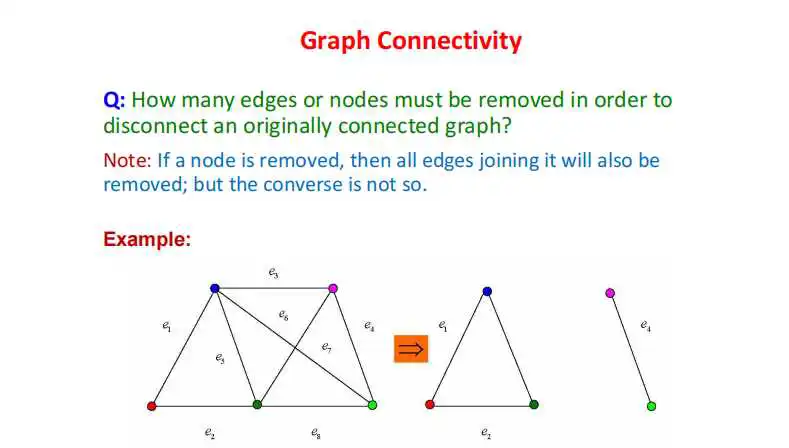
连通性有各种指标。常用的一个,我们来看一看,如果你攻击上图中的左图,比如说把一些连边打掉,也就是说把它们删掉,让图变得不连通,你的攻击就算成功了。实际上,你要拿掉多少条边和拿掉哪一些连边,是要研究一下的事情。研究这些事情,那就分出了两个概念,视频里作详细解释。
接下来是closeness,就是有多靠近,下面视频解释。
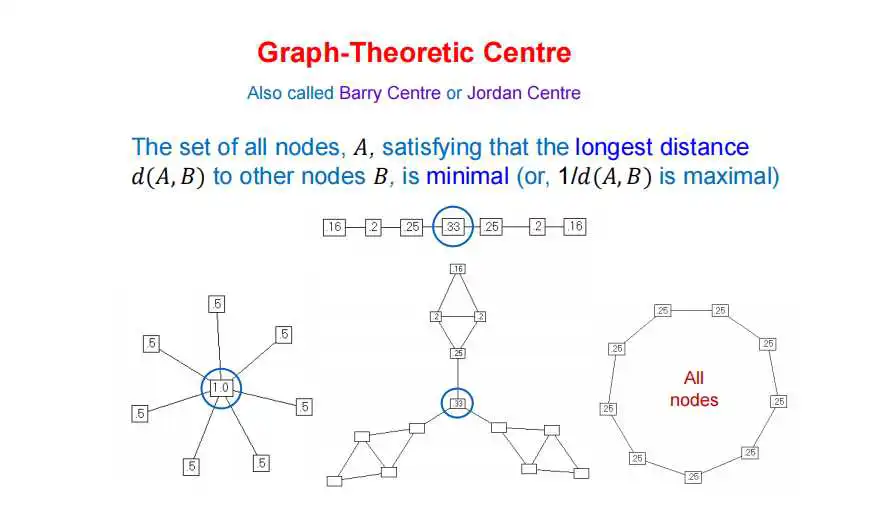
接下来一个,理论稍微难一些,讲的是图理论的中心性。你给我一幅图,你问我这幅图的中心在哪里。什么物理意义都没有,那么中心是怎么来定义的呢?你就看,每一个节点到别的节点的最远距离是多少?比如说,下面顶上的图是一条链,它最左边到最右边最远的距离是6,这个节点嘛最远是3,那个节点呢最远是5,等等。然后,中心节点就定义为那些到别的节点最远距离里面是最短的节点。那我选这个就是对的了,最远距离是3,比任何其它节点到别的节点的最远距离都要小,或者相等。这样的节点就是图理论中心节点,简称中心。有的时候你要小心,图的中心不见得就在图形看上去的中间。如果图不对称,你找不到中间的。对称的话也不见得容易找。而且可能不唯一,例如一个环,每个节点都是中心。你要按照定义去找。
- 陈关荣丨图论基础(上)
- 陈关荣丨网络基本模型与拓扑特征分析(下)
- 陈关荣丨有趣的网络科学!(下篇)
到此这篇gjk算法(gjk算法求距离)的文章就介绍到这了,更多相关内容请继续浏览下面的相关推荐文章,希望大家都能在编程的领域有一番成就!
版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/bcyy/36475.html