本节,我们来看广度优先搜索。在开始记录之前,我们先来看一些小技巧:
在一些题目中,我们经常需要在二维网格中进行四向移动(上下左右地走),这四个方向可以用一个二维向量来表示:
- 左:
- 上:
- 右:
- 下:
大部分时候我们会使用一个二维数组来表示这四个向量(或者两个一维数组)。
但其实也可以将这四个二维向量的 和 坐标连续地放在一个一维数组中,形成一个移动向量数组:
这样,我们就可以通过一个索引 来方便地获取到一个方向的向量。举个栗子,对于当前坐标 ,我们可以通过以下方式来进行移动:
这种方法的优点是代码简洁,易于理解,同时也减少了代码的冗余。在处理二维平面的移动问题时非常实用。
广度优先搜索(BFS)是一种常见的图遍历算法,它的特点是按照“先进先出”的原则访问节点,因此我们通常会使用队列来存储待访问的节点。
我们通常会使用如下的队列来存储待访问的节点:
然后使用来添加新的待访问节点,使用来获取并移除下一个待访问的节点。
但在一些笔试或者竞赛中,我们也会选择使用数组来模拟队列。具体的,我们可以使用一个二维数组来存储待访问的节点,使用两个指针和来分别表示队列的头部和尾部。
然后可以使用如下的方法来添加新的待访问节点:
使用如下的方法来获取并移除下一个待访问的节点:
这里的 和 分别代表队列的头部和尾部的索引:
- 当我们向队列中添加一个元素时,我们将元素添加到索引为 的位置,然后将 加一,表示队列尾部向后移动了一位。
- 同理,当我们从队列中取出一个元素时,我们取出索引为 的元素,然后将 加一,表示队列头部向后移动了一位。
因此,这里的 操作是为了模拟队列的这种行为。
好了,基本介绍已完毕,下面来看看广度优先搜索的题目吧。
广度优先搜索(Breadth-First Search,简称BFS)是一种用于遍历或搜索树或图的算法。这个算法从图的某一节点(或树的根)开始,访问其所有相邻的节点,然后对每个相邻节点,再访问它们的未被访问过的邻节点,以此类推,直到所有节点都被访问过。
广度优先搜索的特点就是“先宽后深”,也就是先访问离起始节点最近的节点,然后再访问离起始节点次近的节点,因此,我们可以用队列来实现这个算法。每次将一个节点的所有邻节点加入队列,然后从队列中取出节点进行访问。
说白了,我们可以将广度优先搜索理解为“水波扩散”,想象一下,你在一个平静的湖面上扔了一块石头,石头落入水面的那一点,就像是广度优先搜索的起始节点。石头落水后,水面会形成一圈圈扩散开去的波纹,每一圈波纹就像是从起始节点开始,经过相同步数可以到达的所有节点。
波纹总是先覆盖离落水点最近的水面,然后再逐渐扩散到更远的地方,这就像广度优先搜索先访问离起始节点最近的节点,再访问离起始节点次近的节点,依次类推。
广度优先搜索在很多问题中都有应用,例如求解最短路径问题、检查图是否连通、求解迷宫问题等,我们在后面的题目会逐渐看到这些例子。
广度优先搜索通用的伪代码如下:
- 创建一个队列 和一个集合/哈希表 用于记录已访问过的节点
- 将起始节点 加入到队列 和集合 中
- 当队列 不为空时,执行以下操作:
- 从队列 中取出一个节点,称为当前节点
- 检查当前节点是否是目标节点。如果是,我们找到了目标,可以结束搜索
- 如果当前节点不是目标节点,那么访问它的所有未访问过的邻居节点,将这些邻居节点加入到队列 和集合 中
- 如果队列 为空,但我们还没有找到目标节点,那么目标节点不可达
记录:
- 在竞赛中,上述的队列以及集合/哈希表基本上都会使用数组来实现。当然也可以使用Java的集合类(偷懒一下)。
- 哈希表有啥用?在 BFS 进行时,进入队列的节点需要标记状态,防止同一个节点重复进出队列。我们不希望节点在扩展的时候又回到上游,周而复始地扩展,因此需要标记一下访问状态。
- 难点:虽然 BFS 是一个理解难度很低的算法,但是其难点在于节点如何找到路、路的展开和以及剪枝设计。这些都需要根据具体的问题来进行设计和实现。
下面,我们来实战一波。
洛谷链接:迷宫寻路
题目描述
机器猫被困在一个矩形迷宫里。
迷宫可以视为一个 矩阵,每个位置要么是空地,要么是墙。机器猫只能从一个空地走到其上、下、左、右的空地。
机器猫初始时位于 的位置,问能否走到 位置。
输入格式
第一行,两个正整数 。
接下来 行,输入这个迷宫。每行输入一个长为 的字符串, 表示墙, 表示空地。
输出格式
仅一行,一个字符串。如果机器猫能走到 ,则输出 ;否则输出 。
样例输入 #1
样例输出 #1
提示
路线如下:
数据规模与约定:
对于 的数据,保证 ,且 和 均为空地。
解题思路:
这道题就是最经典的模板题,也有其他的解法,比如深搜(dfs)。
这节我们来看看用广搜怎么做。

题目要求是,从源点 出发,看是否能够到达 位置。
解题步骤如下:
- 初始化队列和访问标记数组。队列用于存储待访问的节点,访问标记数组用于记录每个位置是否被访问过。
- 将起点加入队列,并标记为已访问。
- 当队列不为空时,从队列中取出一个节点。
- 如果这个节点是终点,那么输出"Yes"并结束程序。
- 如果这个节点不是终点,那就扩展,按照四个方向(左、上、右、下)进行扩展,获取邻居节点。
- 如果某个方向是可行的(即邻居在迷宫内、是空地、并且没有被访问过),那么将其加入队列,并标记为已访问。
- 如果遍历完所有可达的节点都没有找到终点,那么输出"No"。
AcWing 链接:01 矩阵
给定一个 的 矩阵:
定义 与 之间的距离为 。对于每个元素 ,请求出与它距离最近且值为 的元素 和它的距离是多少。
另外注意,当元素 本身就为 时,与它距离最近且值为 的元素就是它自己,距离为 。
输入格式
第一行为两个整数,分别代表 和 。接下来的 行,第 行的第 个字符代表 。
输出格式
共 行,第 行的第 个数字表示 与其距离最近且值为 的元素的距离。
数据范围
输入样例:
输出样例:
解题思路:
这道题就是很典型的广度优先搜索模板题。如何求解?
说白了,就是从值为1的元素开始搜索,然后逐步向外扩展,直到所有元素都被访问过。
实际编码时:
- 我们准备一个队列 ,用于存储待访问的元素,准备一个二维数组 ,用于存储每个元素到最近的 的距离
- 然后遍历一遍:
- 将图中所有值为 的元素加入到队列中,这些值为 的元素就是搜索的起始点。
- 同时,在遍历的过程中:
- 如果元素值为 ,就将数组中对应位置设为 ,表示与它距离最近且值为 的元素就是它自己,距离为 。
- 如果元素值为 ,就将数组中对应位置设为 ,表示该位置未设置过。
- 接着初始化一个计数器 为 ,用于记录当前的距离。
- 当队列不为空时,执行以下操作:
- 增加计数器
- 获取当前队列的大小
- 对于队列中的每个元素,执行以下操作:
- 取出队列中的元素
- 访问该元素的四个方向的邻居
- 如果邻居在边界内并且其距离为,那么更新其距离为 ,并将其添加到队列中
- 结束
参考代码如下:
我们再来看这道力扣题,也是一道模板题:
力扣链接:1162. 地图分析
你现在手里有一份大小为 的 网格 ,上面的每个 单元格 都用 和 标记好了。其中 代表海洋, 代表陆地。
请你找出一个海洋单元格,这个海洋单元格到离它最近的陆地单元格的距离是最大的,并返回该距离。如果网格上只有陆地或者海洋,请返回 。
我们这里说的距离是「曼哈顿距离」( Manhattan Distance): 和 这两个单元格之间的距离是 。
示例 1:

示例 2:

示例 1:
示例 2:
提示:
- 不是 就是
解题思路:
很简单,我们首先将所有的陆地单元格加入到队列中,然后从这些陆地单元格开始,一层一层地向外扩展,直到所有的海洋单元格都被访问到。在这个过程中,我们可以记录下每个海洋单元格到最近的陆地单元格的距离,最后返回这些距离中的最大值。
算法步骤:
- 初始化一个队列,将所有的陆地单元格加入到队列中。
- 初始化一个二维数组,用于记录每个海洋单元格到最近的陆地单元格的距离。
- 进行广度优先搜索,每次从队列中取出一个单元格,然后访问它的上下左右四个相邻的单元格。如果相邻的单元格是海洋,并且还没有被访问过,那么就将它加入到队列中,并更新它到最近的陆地单元格的距离。
- 最后,遍历所有的海洋单元格,找出距离最大的那个,返回其距离。
参考代码:
这段代码首先将所有的陆地单元格加入到队列中,然后进行广度优先搜索,每次从队列中取出一个单元格,然后访问它的上下左右四个相邻的单元格。如果相邻的单元格是海洋,并且还没有被访问过,那么就将它加入到队列中,并更新它到最近的陆地单元格的距离。最后,返回最大的距离。
AcWing 链接:01 矩阵
栋栋最近开了一家餐饮连锁店,提供外卖服务。
随着连锁店越来越多,怎么合理的给客户送餐成为了一个急需解决的问题。
栋栋的连锁店所在的区域可以看成是一个 的方格图(如下图所示),方格的格点上的位置上可能包含栋栋的分店(绿色标注)或者客户(蓝色标注),有一些格点是不能经过的(红色标注)。
方格图中的线表示可以行走的道路,相邻两个格点的距离为 1。
栋栋要送餐必须走可以行走的道路,而且不能经过红色标注的点。
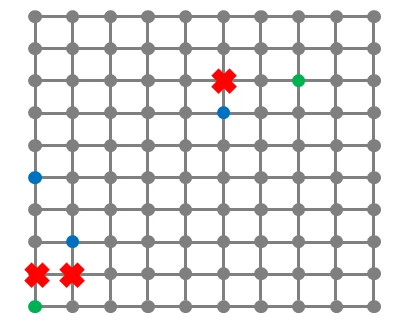
送餐的主要成本体现在路上所花的时间,每一份餐每走一个单位的距离需要花费 块钱。
每个客户的需求都可以由栋栋的任意分店配送,每个分店没有配送总量的限制。
现在你得到了栋栋的客户的需求,请问在最优的送餐方式下,送这些餐需要花费多大的成本。
输入格式
输入的第一行包含四个整数 ,分别表示方格图的大小、栋栋的分店数量、客户的数量,以及不能经过的点的数量。
接下来 行,每行两个整数 ,,表示栋栋的一个分店在方格图中的横坐标和纵坐标。
接下来 行,每行三个整数 ,,,分别表示每个客户在方格图中的横坐标、纵坐标和订餐的量。(注意,可能有多个客户在方格图中的同一个位置)
接下来 行,每行两个整数,分别表示每个不能经过的点的横坐标和纵坐标。
输出格式
输出一个整数,表示最优送餐方式下所需要花费的成本。
数据范围
前 的评测用例满足:。
前 的评测用例满足:。
所有评测用例都满足:,,。
可能有多个客户在同一个格点上。
每个客户的订餐量不超过 ,每个客户所需要的餐都能被送到。
输入样例:
输出样例:
解题思路:
这道题也不难,主要思路是从每个分店出发,通过BFS找到每个客户的最短路径,计算总的配送成本。
解题步骤:
- 初始化一个二维数组 来存储每个位置到分店的最短距离,初始值设为无穷大。同时,初始化一个二维数组 来表示每个位置是否可以通行,初始值设为 。
- 读取分店的坐标,将分店的位置加入队列,并将 中对应的距离设为 0。
- 读取客户的信息,包括坐标和订餐量,存入 数组。
- 读取不能通行的位置,将 中对应的值设为 。
- 进行BFS。从队列中取出一个位置,遍历其四个方向的邻居。如果邻居在图中并且可以通行,且从当前位置到邻居的距离小于 中存储的距离,就更新 中的距离,并将邻居加入队列。
- BFS结束后,遍历每个客户,将 中对应的距离乘以订餐量,累加得到总的配送成本。
参考代码:
力扣链接:691. 贴纸拼词
我们有 种不同的贴纸。每个贴纸上都有一个小写的英文单词。
您想要拼写出给定的字符串 ,方法是从收集的贴纸中切割单个字母并重新排列它们。如果你愿意,你可以多次使用每个贴纸,每个贴纸的数量是无限的。
返回你需要拼出 的最小贴纸数量。如果任务不可能,则返回 。
注意: 在所有的测试用例中,所有的单词都是从 个最常见的美国英语单词中随机选择的,并且 被选择为两个随机单词的连接。
示例 1:
示例 2:
提示:
- 和 由小写英文单词组成
解题思路:
这道题有很多种解法(比如动态规划,深度优先搜索等)。
现在,我们关注,怎么用BFS来解决这道题。首先,我们可以发现,将字符串(target)排个序,是不会影响最终结果,现在我们只考虑使用哪些贴纸,最终能拼接出target(即使贴纸有剩余的字符也没事),那么思路来了:
我们将target作为搜索的起始点,然后每次都尝试使用一个贴纸去匹配并消除target中的字符,然后得到一个新字符串(逐渐匹配,消除,展开到下一层),将新的字符串作为待访问的元素加入到队列中,然后继续扩展,直到目标字符串target变为空字符串,就意味着我们找到了答案,此时返回展开的层数即可。
步骤如下:
- 初始化一个队列和一个访问集合。队列用于存储待处理的字符串,访问集合用于记录已经处理过的字符串,避免重复处理。
- 将所有贴纸和目标字符串按字母排序,并将每个贴纸的首字母对应的贴纸列表存入图中。
- 将目标字符串加入队列和访问集合,然后开始宽度优先搜索。
- 在每一轮搜索中,从队列中取出一个字符串,然后遍历与该字符串首字母对应的所有贴纸,尝试使用贴纸消除字符串中的字符。消除字符的方法是,同时遍历字符串和贴纸,如果字符相同,则同时向后移动,否则只移动字符串的指针。
- 如果消除字符后的字符串为空,说明已经完全匹配,返回当前的贴纸数量。如果字符串不为空且未被访问过,则将其加入队列和访问集合,等待下一轮处理。
- 如果队列为空,说明无法匹配目标字符串,返回-1。
参考代码:
刷到这里,相信你已经初步熟悉了 BFS 的解题套路,下面可以去各大刷题网站刷一下BFS的题目巩固一下吧。
到此这篇广度优先搜索实例(广度优先搜索例题)的文章就介绍到这了,更多相关内容请继续浏览下面的相关推荐文章,希望大家都能在编程的领域有一番成就!版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/bcyy/36833.html
