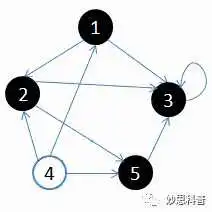
图是一种灵活的数据结构,一般作为一种模型用来定义对象之间的关系或联系。对象由顶点(V)表示,而对象之间的关系或者关联则通过图的边(E)来表示。
图可以分为有向图和无向图,一般用G=(V,E)来表示图。经常用邻接矩阵或者邻接表来描述一副图。
在图的基本算法中,最初需要接触的就是图的遍历算法,根据访问节点的顺序,可分为广度优先搜索(BFS)和深度优先搜索(DFS)。
广度优先搜索(BFS)
广度优先搜索在进一步遍历图中顶点之前,先访问当前顶点的所有邻接结点。
a .首先选择一个顶点作为起始结点,并将其染成灰色,其余结点为白色。
b. 将起始结点放入队列中。
c. 从队列首部选出一个顶点,并找出所有与之邻接的结点,将找到的邻接结点放入队列尾部,将已访问过结点涂成黑色,没访问过的结点是白色。如果顶点的颜色是灰色,表示已经发现并且放入了队列,如果顶点的颜色是白色,表示还没有发现
d. 按照同样的方法处理队列中的下一个结点。
基本就是出队的顶点变成黑色,在队列里的是灰色,还没入队的是白色。
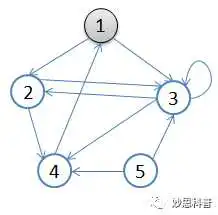
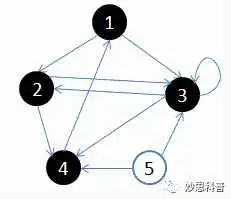
用一副图来表达这个流程如下:
1.初始状态,从顶点1开始,队列={1}
2.访问1的邻接顶点,1出队变黑,2,3入队,队列={2,3,}
3.访问2的邻接结点,2出队,4入队,队列={3,4}
4.访问3的邻接结点,3出队,队列={4}
5.访问4的邻接结点,4出队,队列={ 空}
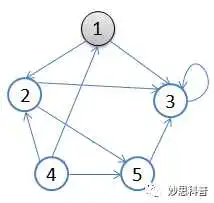
从顶点1开始进行广度优先搜索:
- 初始状态,从顶点1开始,队列={1}访问1的邻接顶点,1出队变黑,2,3入队,队列={2,3,}
- 访问2的邻接结点,2出队,4入队,队列={3,4}
- 访问3的邻接结点,3出队,队列={4}
- 访问4的邻接结点,4出队,队列={ 空}
- 结点5对于1来说不可达。
上面的图可以通过如下邻接矩阵表示:
int maze[5][5] = {
{ 0, 1, 1, 0, 0 },
{ 0, 0, 1, 1, 0 },
{ 0, 1, 1, 1, 0 },
{ 1, 0, 0, 0, 0 },
{ 0, 0, 1, 1, 0 }
};
BFS核心代码如下:
#include <iostream>
#include <queue>
#define N 5
using namespace std;
int maze[N][N] = {
{ 0, 1, 1, 0, 0 },
{ 0, 0, 1, 1, 0 },
{ 0, 1, 1, 1, 0 },
{ 1, 0, 0, 0, 0 },
{ 0, 0, 1, 1, 0 }
};
int visited[N + 1] = { 0, };
void BFS(int start)
{
queue<int> Q;
Q.push(start);
visited[start] = 1;
while (!Q.empty())
{
int front = Q.front();
cout << front << " ";
Q.pop();
for (int i = 1; i <= N; i++)
{
if (!visited[i] && maze[front - 1][i - 1] == 1)
{
visited[i] = 1;
Q.push(i);
}
}
}
}
int main()
{
for (int i = 1; i <= N; i++)
{
if (visited[i] == 1)
continue;
BFS(i);
}
return 0;
}
深度优先搜索(DFS)
深度优先搜索在搜索过程中访问某个顶点后,需要递归地访问此顶点的所有未访问过的相邻顶点。
初始条件下所有节点为白色,选择一个作为起始顶点,按照如下步骤遍历:
a. 选择起始顶点涂成灰色,表示还未访问
b. 从该顶点的邻接顶点中选择一个,继续这个过程(即再寻找邻接结点的邻接结点),一直深入下去,直到一个顶点没有邻接结点了,涂黑它,表示访问过了
c. 回溯到这个涂黑顶点的上一层顶点,再找这个上一层顶点的其余邻接结点,继续如上操作,如果所有邻接结点往下都访问过了,就把自己涂黑,再回溯到更上一层。
d. 上一层继续做如上操作,知道所有顶点都访问过。
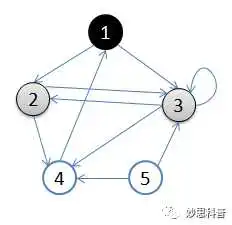
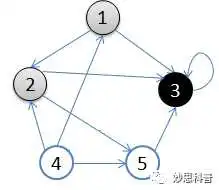
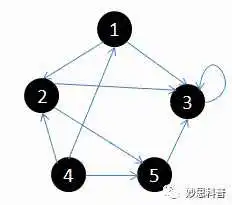
用图可以更清楚的表达这个过程:
1.初始状态,从顶点1开始
2.依次访问过顶点1,2,3后,终止于顶点3
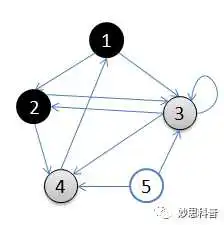
3.从顶点3回溯到顶点2,继续访问顶点5,并且终止于顶点5
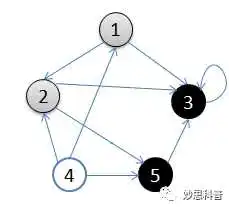
4.从顶点5回溯到顶点2,并且终止于顶点2
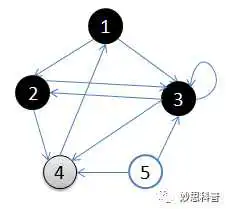
5.从顶点2回溯到顶点1,并终止于顶点1
6.从顶点4开始访问,并终止于顶点4
- 从顶点1开始做深度搜索:初始状态,从顶点1开始依次访问过顶点1,2,3后,终止于顶点3
- 从顶点3回溯到顶点2,继续访问顶点5,并且终止于顶点5
- 从顶点5回溯到顶点2,并且终止于顶点2
- 从顶点2回溯到顶点1,并终止于顶点1
- 从顶点4开始访问,并终止于顶点4
上面的图可以通过如下邻接矩阵表示:
int maze[5][5] = {
{ 0, 1, 1, 0, 0 },
{ 0, 0, 1, 0, 1 },
{ 0, 0, 1, 0, 0 },
{ 1, 1, 0, 0, 1 },
{ 0, 0, 1, 0, 0 }
};
DFS核心代码如下(递归实现):
#include <iostream>
#define N 5
using namespace std;
int maze[N][N] = {
{ 0, 1, 1, 0, 0 },
{ 0, 0, 1, 0, 1 },
{ 0, 0, 1, 0, 0 },
{ 1, 1, 0, 0, 1 },
{ 0, 0, 1, 0, 0 }
};
int visited[N + 1] = { 0, };
void DFS(int start)
{
visited[start] = 1;
for (int i = 1; i <= N; i++)
{
if (!visited[i] && maze[start - 1][i - 1] == 1)
DFS(i);
}
cout << start << " ";
}
int main()
{
for (int i = 1; i <= N; i++)
{
if (visited[i] == 1)
continue;
DFS(i);
}
return 0;
}
非递归实现如下,借助一个栈:
#include <iostream>
#include <stack>
#define N 5
using namespace std;
int maze[N][N] = {
{ 0, 1, 1, 0, 0 },
{ 0, 0, 1, 0, 1 },
{ 0, 0, 1, 0, 0 },
{ 1, 1, 0, 0, 1 },
{ 0, 0, 1, 0, 0 }
};
int visited[N + 1] = { 0, };
void DFS(int start)
{
stack<int> s;
s.push(start);
visited[start] = 1;
bool is_push = false;
while (!s.empty())
{
is_push = false;
int v = s.top();
for (int i = 1; i <= N; i++)
{
if (maze[v - 1][i - 1] == 1 && !visited[i])
{
visited[i] = 1;
s.push(i);
is_push = true;
break;
}
}
if (!is_push)
{
cout << v << " ";
s.pop();
}
}
}
int main()
{
for (int i = 1; i <= N; i++)
{
if (visited[i] == 1)
continue;
DFS(i);
}
return 0;
}
有的DFS是先访问读取到的结点,等回溯时就不再输出该结点,也是可以的。算法和我上面的区别就是输出点的时机不同,思想还是一样的。DFS在环监测和拓扑排序中都有不错的应用。
PS: 图文均为本人原创,画了好几个小时,转载注明出处,尊重知识劳动,谢谢~

版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/bcyy/54814.html