
数最原始的功能就是比较大小,数不能比较大小,就没有存在的必要了。下面说说比较复杂的数比较大小。
新高考对数和指数比较大小的问题
近一段时间以来,高考数学试卷越来越多的出现了许多比较大小的题型,我们发现常用的一些方法比如单调性法,引入中间变量法等好像作用比较小,需要挖掘更多的方法,比如放大缩小法,构建函数法,糖水不等式法等方法,或者需要对原来的方法加以强化,下面看一下最近一些比较复杂的比较大小问题。
一、没想到f(x)=ln(lg(x)),g(x)=lg(ln(x))是增函数,而且大小关系能判断。
例: 如下题目:
比较大小
[解析]:对于题目中的 对应的函数 , 定义域为 时,
复合函数 都是增函数, 我们看看 的单调性,
因为ln10-1>0,当x>=1时,lnx>0,所以h(x)递增,
当x=e时,h(e)<0
当x=10时,h(10)=ln(lg10)-lg(ln10)=-lg(ln10)<0
因为 , 所以 , 即 至于 与 ,
所以 , 对于 与 , 设 , 因为递增, 且 ,
结论:
当x>1时,F(x)=ln(lgx),g(x)=lg(lnx),h(x)=ln(lgx)-lg(lnx)都为增函数,h(x)的零点为近似值为79左右的值。对于零点可以试探性的确定。
二、利用f(x)=lnx/x函数,处理含lnx的问题比较有效
例题: (2005 全国二理 6) 比较大小
解: 在 递增, 递减, , 由 , 所以 .
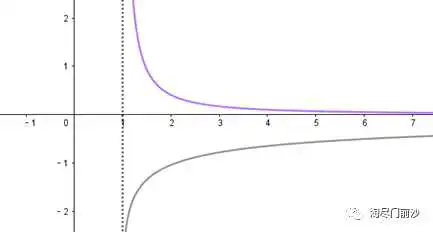
变式训练: 8
解: 根据 在 递减, 由 ,
所以
三、 其实是个減函数, 其实是个增函数,可以衍生糖水多项式。
对于函数 , 且 ,
对于函数 , 当 递减; 当 递增。所以对于函数 显然, 时, 所以 递减。类似的 , 当 时, 递增。
若 , 且 ,
时, 递减。
类似若 , 且 时, 递增。
可推出常用结论:
(1) (2) (3) 更一般的:
,
由糖水不等式 <a
类比, 上面式子可以看作是对数型糖水不等式。
例:比较大小 (1) ; (2) 解析: (1) ; (2) 变式训练 : 比较大小
(提示:利用性质+换底做差法解决。)
例题 : (2021 全国乙卷, 12) 设 ,比较大小关系。
解析:此题难道还是有的,先比较a与b,
与 比较大小, 今 ,构造函数法,
由图像, 递增, 递减, 所以 用泰勒展开式能估算吗?
即 . 最后得到: 与 如何比较呢: 构造函数法试一下:
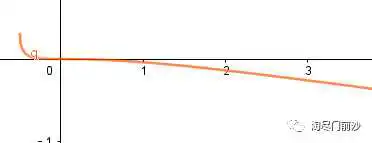
所以b<c.
结论:2021年两个数比较大小主要体现了构造函数法比较大小的作用。用其他的办法都比较复杂。
四、贝努力不等式合理利用,能解决指数的比较大小。
公式如下:

事实上,用计算器算一下,差别还是很小的。
结论:除利用了前面讲到的对数型糖水不等式以外,还用到了贝努力不等式,贝努力不等式在用法比较灵活,要学会把x变小,不能太大。

版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/bcyy/71297.html
