argparse什么意思（argos是什么意思）

今天杜老师给大家科普一个“条件概率”里常常会用到的定律—“贝叶斯定律”，虽然在咱GRE数学的学习过程中，该定律很少会被拿来破题（着实大材小用），但是了解贝叶斯定律相信会有助于大家对条件概率的理解更上一层楼。

首先不管大家认不认识先请出贝叶斯定律：

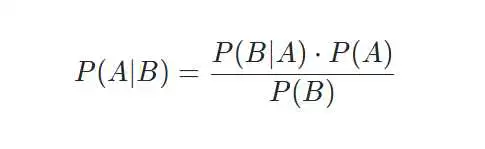
当然我个人习惯这样写：

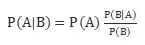
接着问题来了，什么是贝叶斯定理呢？

通俗来说就是：在信息和条件有限的情况下，基于过去的数据，通过动态调整的方法，帮助我们逐步预测出事件发生的接近真实概率。

这一过程可以形象地理解为：我们首先根据已有的背景知识或历史数据形成一个初始判断，即先验概率（也就是上文的P(A)）；之后随着新证据的出现，我们会不断修正这个判断，通过乘以一个调整因子(也就是上文的 P(B|A) / P(B) )，最终得到一个更准确的预测结果，即后验概率(即：P(A|B) )。

贝叶斯公式正是这一过程背后的数学表达式。它允许我们在获取新的信息后，重新评估先前的概率估计，从而更加接近实际发生的概率。

这种从先验到后验的转变，不仅体现了统计学中的一个重要原则—利用新数据不断更新我们的认知，而且也揭示了概率论在解决不确定性和复杂性问题时的巨大潜力。

首先，我们假设一些事件：

A事件：取1个球，球来自1号盒。

B事件：抓取的是白球。
C事件：取1个球，球来自2号盒。

然后我们来分析一下题目，很明显题目让我们做一件事—算概率，但是有两个要求：①球得来自一号盒，②已知球是白球。我们先来解决要求①，这一步很简单，总共40个球，一号盒20个球，故P(A)=50%。

但很明显50%不能作为答案，因为题目对被取出来的这个球有更严苛的要求即【白色】，所以我需要在P(A)，即50%的基础上进行一些调整，那么这里的“调整”在贝叶斯定律里称之为“调整函数/因子”，也就是说最后题目让我们算的结果应该等于【先验概率】×【调整因子】；那么这个调整因子怎么求呢？

往下看，这是固定的求法：

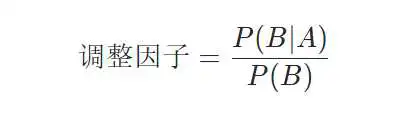
这个表达式说明了在事件A发生的情况下，事件B发生的概率与事件B发生的总概率之间的比例关系。

那么对应我们这道题例题，P(B|A)的意思就是说已知球来自于一号盒的情况下，取出白球的概率；P(B)的意思是说取出所有白球的总概率。

了解意思之后，我们开始算一下P(B|A)=15/20=75%，P(B)即白球总概率，它等于一号盒中取出白球和二号盒中取出白球两个事件的概率之和，即 75% *50% + 50% * 50%= 62.5% （注：取球前先得取盒子，盒子二取一所以是50%），所以最后调整因子等于75%/62.5%，即1.2。

也就是说：取一个球，没有其他约束条件时，该球来自于一号盒的概率是50%；而当我得知取出来的球是白球时，那么该球来自于一号盒子的概率提高至20%，因为调整因子是1.2（其实因为两盒中白球的权重不同，一号盒的白球权重更大，所以当我得知球的颜色是白球的时候，我们也会本能的怀疑该球是不是更大概率的来自一号盒，而贝叶斯定律则可以帮我们量化所谓的“大概率”）。

所以最后算出来的概率=50%×1.2=60%

贝叶斯公式的核心在于将先验概率与新证据相结合，从而得出更加精确的后验概率。这一过程不仅展示了概率论在处理不确定性问题中的强大能力，其实也可以广义的延伸至为我们在日常生活中遇到的各种决策去提供科学指导。

好了！今天的分享就先到这了，我们下期见！