一、 问题的提出
某导弹基地发现正北方向120km处海面上有敌艇一艘以90km/h的速度向正东方向行驶。该导弹基地立即发射一枚导弹跟踪追击敌艇,导弹速度为450km/h,自动导航系统使导弹在任一时刻都能对准敌艇。
(1)试问导弹在何时何处击中敌艇?
(2)如果发射导弹时,敌舰立即由仪器觉察。假定敌舰为一高速快艇,它即刻以135km/h的速度与导弹方向成一夹角逃逸,问导弹何时何地击中敌舰?根据计算结果,你能否指出敌舰与导弹方向成何夹角逃逸才好?
二、 问题的分析
问题一要求计算导弹击中敌舰的位置和时间,探寻导弹的追踪轨迹,首先建立合适的直角坐标系;然后通过将速度分解为水平与竖直两个方向,充分利用导弹和敌舰速度与导弹运动轨迹x,y的联系,建立微分方程组模型;最后,可基于Euler迭代法对模型进行求解,并绘制出导弹的运动轨迹。
问题二要求当敌舰它即刻以135km/h的速度与导弹方向成一夹角逃逸时,要找到导弹何时何地击中敌舰,并指出敌舰与导弹方向成何夹角逃逸才好。可以选取若干特殊逃逸角度进行计算,并通过对比不同角度得到的导弹逃逸结果,获得导弹的最佳逃逸角度与位置。
三、 模型假设
针对以上问题,考虑各种因素对建模的影响,做出如下合理假设:
1.假设导弹调整方向的能力非常强;
2.假设导弹与敌舰相距足够近时敌舰即被击中。
四、 模型的建立
4.1 问题一模型的建立与求解
4.1.1 建立微分方程组
对于第一问,导弹在任一时刻都能对准敌舰,导弹的飞行方向会随着时间t的改变而改变,可以知道导弹的追踪轨迹是一条随着时间变化的曲线,其中曲线上的每一点斜率方向都指向敌。因此,本文建立直角坐标系进行分析,取导弹基地为原点O(0, 0),x轴指向正东方,y轴指向正北方。
导弹从(0, 0)处出发,以450km/h的速度追击敌舰,设其t时刻的坐标为P(x, y),建立如下微分方程组如下:
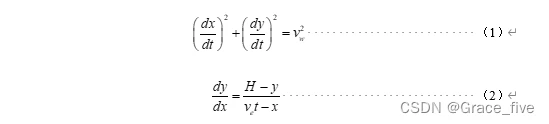
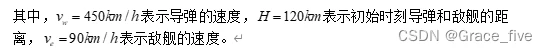
4.1.2 Euler迭代法
在求解微分方程的时候往往计算量很大,甚至无法求解,在解决实际问题时,只需要解出近似值,Euler迭代法是解微分方程常见的数值算法,其思想是将连续变量的微分方程改为离散变量的差分方程。将以上方程组改写为Euler格式:
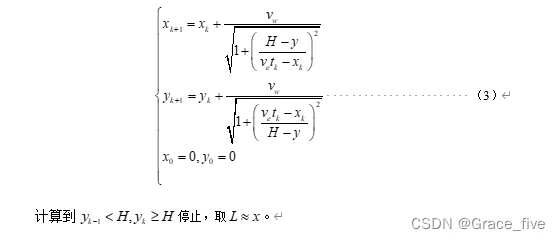
4.1.3 模型的求解
运用Maple 2015求解,程序代码:
程序代码1: h := 0.001; k := 1; L := 120; Ve := 90; Vw := 450; x := [0]; y := [0]; while y[k] <= L do x := [op(x), x[k]+(Ve*t-x[k])*Vw*h/sqrt((Ve*t-x[k])^2+(L-y[k])^2)]; y := [op(y), y[k]+(L-y[k])*Vw*h/sqrt((Ve*h*k-x[k])^2+(L-y[k])^2)]; t := h*k; k := k+1 end do; x[k]; y[k]; t; with(plots); p := plot([seq([x[i], y[i]], i = 1 .. k)]); q := plot([seq([Vs*i*h, L], i = 1 .. k)]); display(p, q) ``
4.1.4 结果分析`
运行该程序可得,得到迭代结果如图1所示,即不同时间导弹的位置。
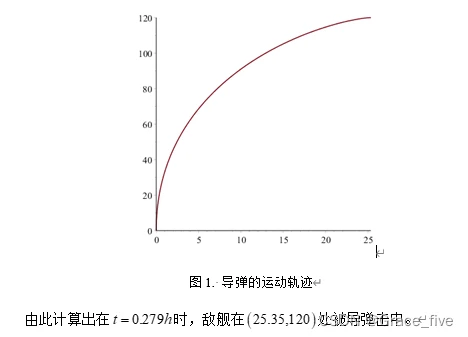
运用Maple 2015求解,程序代码:
程序代码2: H := 120; v1 := 450; v2 := 135; tau := .1; theta := (1/3)*Pi; C1 := evalf(cos(theta)); S1 := evalf(sin(theta)); xd := [0]; yd := [v1*tau]; xj := [v2*tau*S1]; yj := [C1*tau*v2+H]; L1 := [[xd[1], yd[1]]]; L2 := [[xj[1], yj[1]]]; k := 1; d := sqrt((xd[k]-xj[k])^2+(yd[k]-yj[k])^2); while d > 0.03 do C := (xj[k]-xd[k])/sqrt((xj[k]-xd[k])^2+(yd[k]-yj[k])^2): S := (yj[k]-yd[k])/sqrt((xj[k]-xd[k])^2+(yd[k]-yj[k])^2): xd := [op(xd), C*tau*v1+xd[k]]: yd := [op(yd), S*tau*v1+yd[k]]: xj := [op(xj), xj[k]+v2*tau*(C*C1+S*S1)]: yj := [op(yj), yj[k]+v2*tau*(-C*S1+C1*S)]: L1 := [op(L1), [xd[k], yd[k]]]: L2 := [op(L2), [xj[k], yj[k]]]: k := k+1; d := sqrt((xd[k]-xj[k])^2+(yd[k]-yj[k])^2) end do; [xd[k], yd[k]]; 60*k*tau; F := plot(L1); G := plot(L2) 不同特殊角度敌舰被击中的时间与位置如表1。
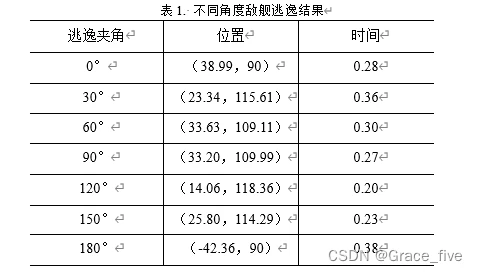
由于敌舰的速度小于导弹的速度,所以敌舰不管与导弹呈何种角度,都不可能摆脱导弹,只能尽可能拖延时间,通过表1不难发现,当敌舰和导弹保持180°角度是,逃逸的时间最长,因此,敌舰可与导弹保持180°,以获得更长时间等待救援。
版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/jszy-gual/10247.html
