点击上方蓝色文字关注我们吧~


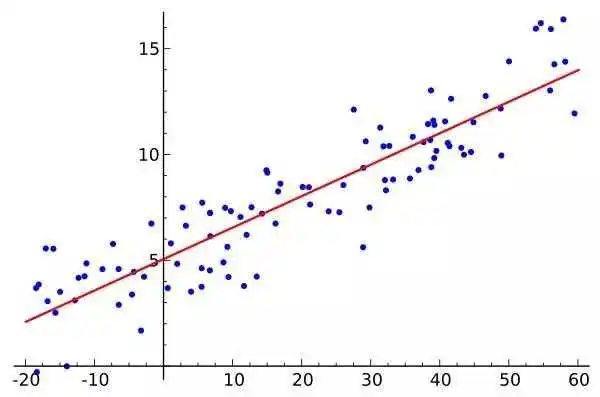
[线性回归方程]设有n个样本(xi,yi)(i=1,2,…,n),散点图大致呈线性。拟合的直线方程为

方程中的系数为,

其中样本x和y的平均值为,

[系数的推导]上述公式仅是回归方程的定义,各类考试一般都是直接给出。而实际应用都采用下述公式,

在现行高中数学课本是没有推导过程的。我们下面来进行推导。
首先证明变形后的两个公式。
对于分子有,

对于分母有,

[方程的推导]接着推导线性回归方程本身。
对于假定的回归方程,如果直接用偏差进行评估,由于偏差有正有负,会相互抵消,所以不能反映采样点与回归方程的接近程度。因此采用n个样本点的平方和进行估计,

当该平方和最小时,就求出了回归方程。因此这种方法又被称为最小二乘估计(LSE, Least Square Estimate)。
将Q展开,并整理有,

然后转化为平均数,有

对a进行配方,有,

最后整理,得

再利用前述的公式,进行变形,得

进一步整理,并配方,有

上式中,前两项为与a,b有关非负项的和,后两项与a,b无关。因此若使得Q最小,令前两项为0即可。即,

将第一项变形,有,

即得所证。
往期精选

扫描二维码关注我
版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/jszy-jnts/50735.html
