方波的四种形式,但我们经常遇见的是左上角和右下角的两种形式,如图14.4所示。
本文引用地址:
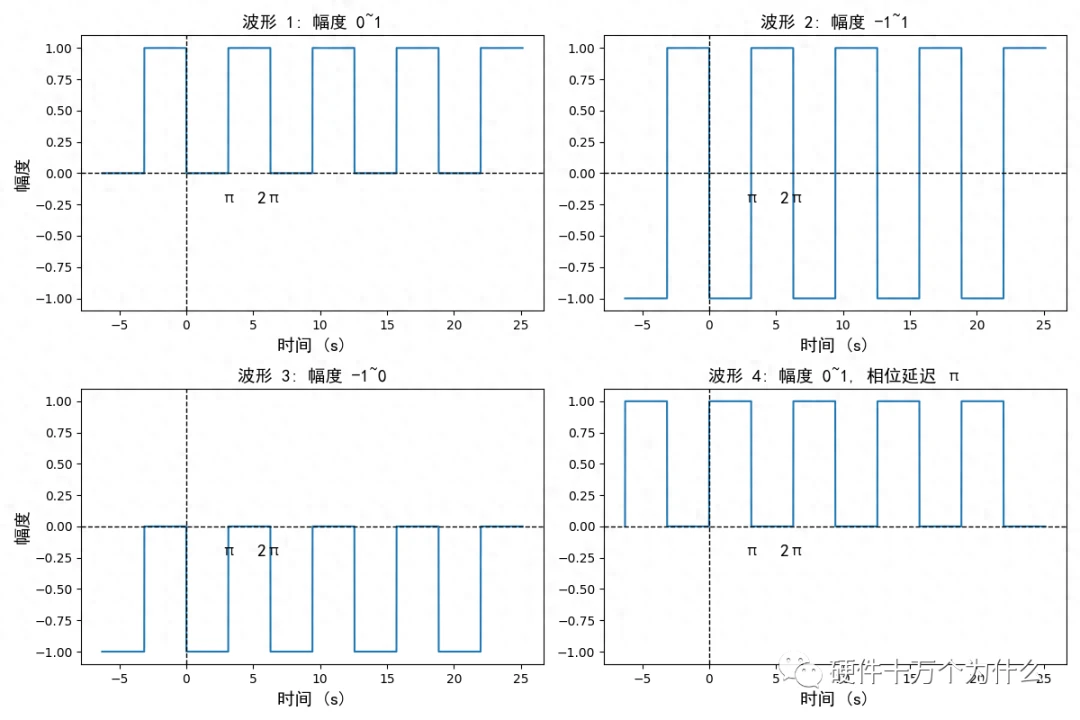
我们就以右下角为例来分析方波函数,

我们可以把积分周期从0~T,移动到-T/2~T/2,因为函数式周期信号,所以两个区间积分的结果一致。
我们根据傅里叶级数系数公式:
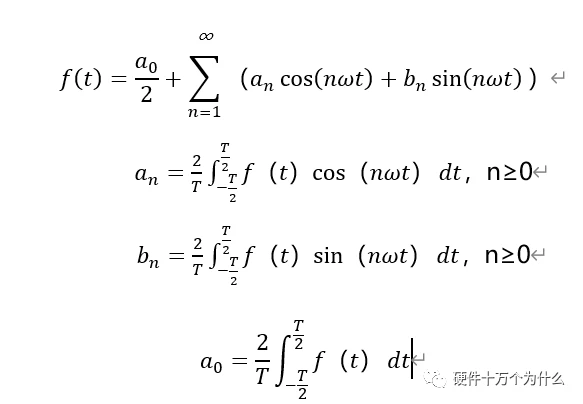




当n为偶函数时,cosnπ=1,则bn=0,当n为奇函数时,cosnπ=0,bn=2A/nπ
任何周期性的信号都可以用无数个正弦函数之和来表示,每个正弦函数分量的频率是基频f0=1/T的倍数。通常,噪声也是随着电路的运转而周期性地存在,因此需要对噪声的特性进行频域上的分析。我们假设周期为T的方波信号,波形如图14.4所示。
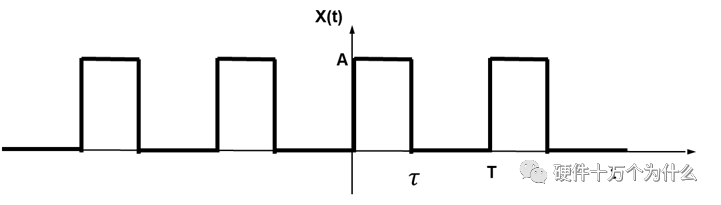
周期为T的方波的三角函数的傅里叶级数可以表示为
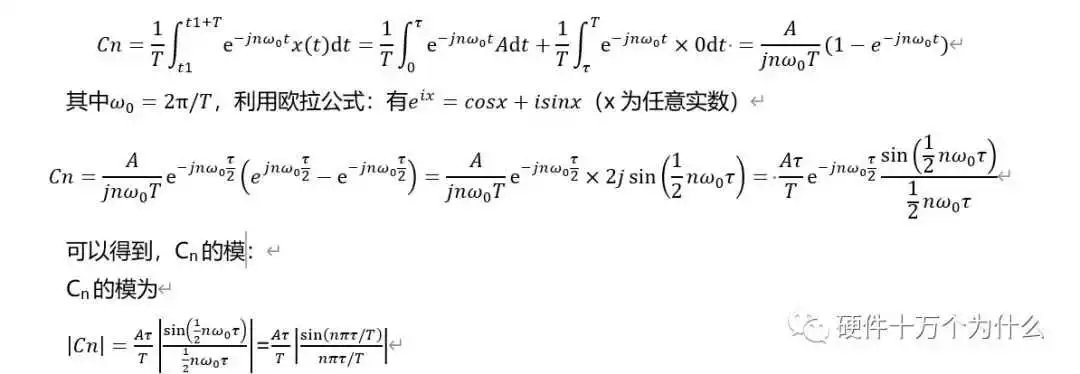
所以可以看到转换到频域,频谱分量只存在在基频f0=1/T的奇数倍(谐波)上。负数频域在实际中不需要考虑,则Cn的频谱特性如图14.5所示。在图中,标注了频谱的包络线。
包络线是一个信号在时域或频域中振荡的峰值点形成的曲线,表示了信号振荡的上下界。包络线通常用于描述一个信号的整体趋势,而忽略了信号内部的高频振荡。包络线提供了一个有效的手段来捕捉信号振荡的整体特征,而不受高频细节的影响。
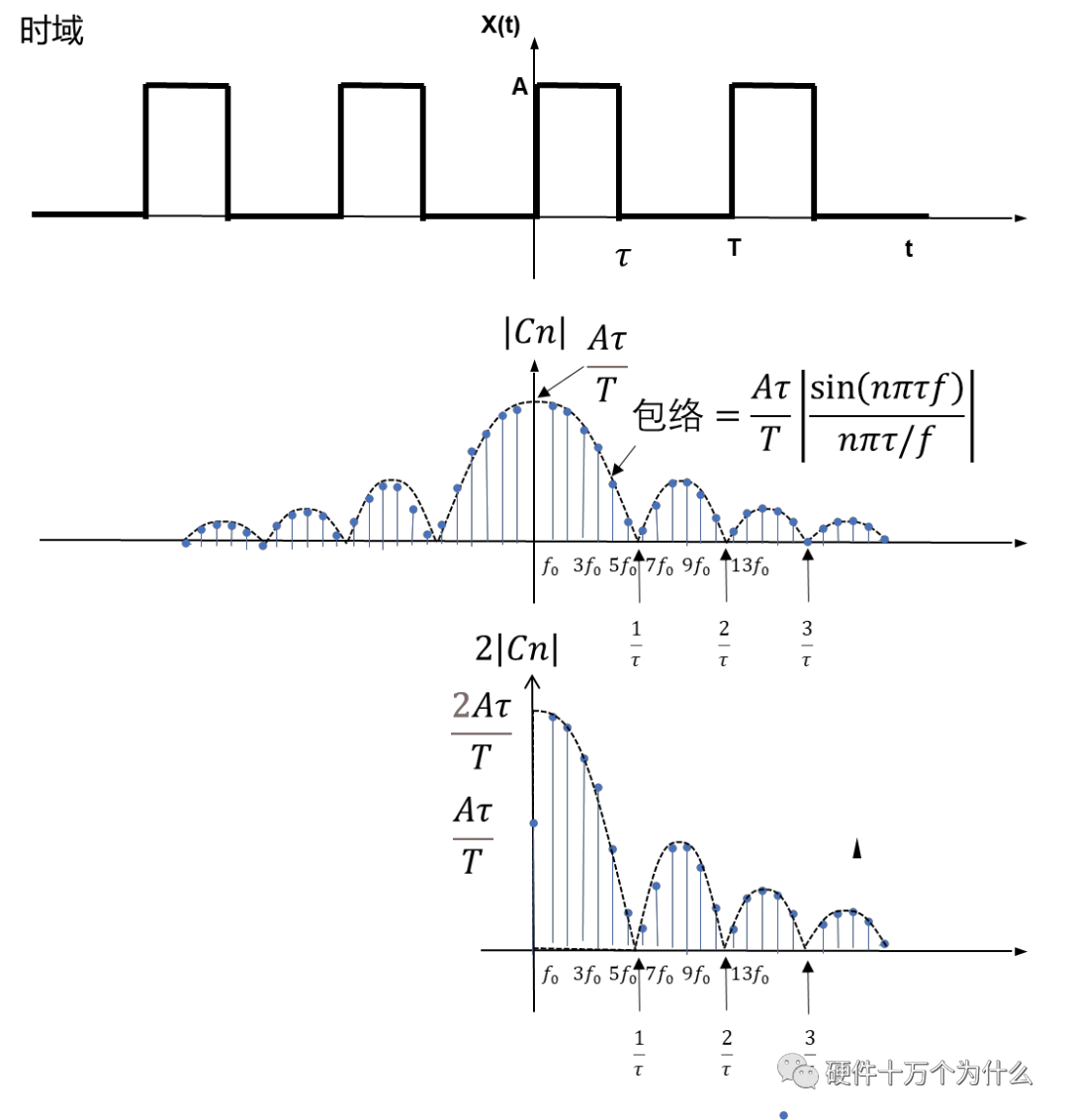
对于50%占空比的方波来说,只包含奇次谐波的分量,偶次谐波的分量为零。对于这个特点,在我们实际的应用中可以加以应用。
以上分析的理想方波,上升时间和下降时间为零,但在实际应用中没有这么理想的方波,甚至我们希望通过减缓上升和下降时间来降低高频的谐波分量。梯形周期脉冲波形如图14.6所示。
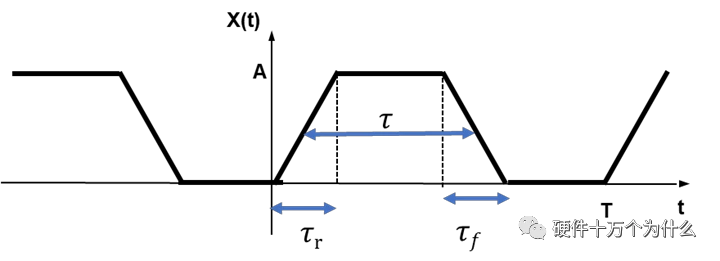
如图的梯形波周期脉冲,原始的展开系数是
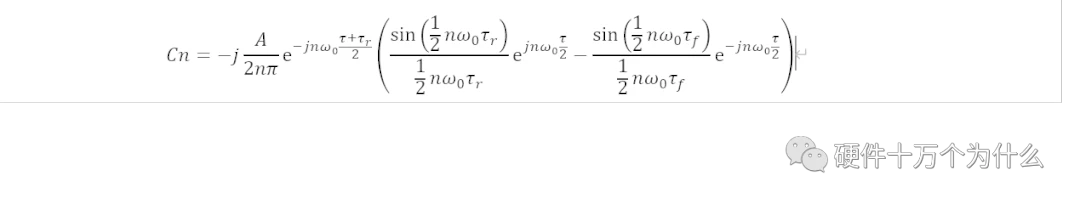
简化分析,我们考虑
的特殊情况,可以进一步合并,得到展开式的系数为,我们用τr来代替τf
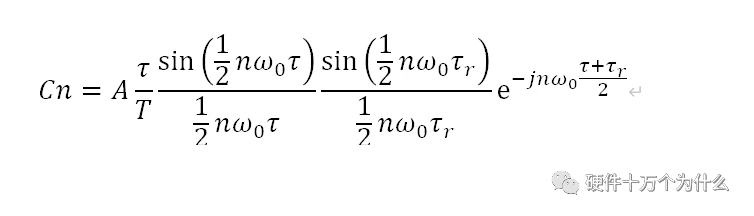
这个展开式对比方波的展开式,是包含两项
的乘积。在方波的分析中,虽然谱分量只存在在
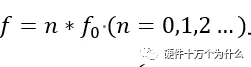
上,但是包络具有的形式,它的边界是确定的。

我们对方波和梯形波的展开系数做对数运算,则两种波形在频谱上体现出梯形波的高频分量明显比方波更小,其高频对外辐射也会更小。
方波的包络,如图14.8(a)所示,形波的包络,如图14.8(b)所示
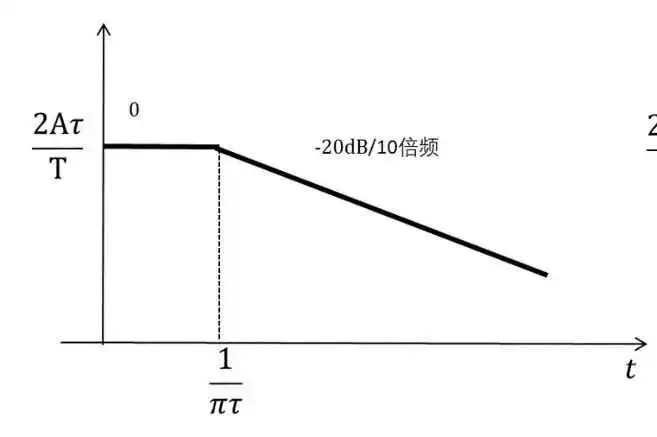
(a)方波
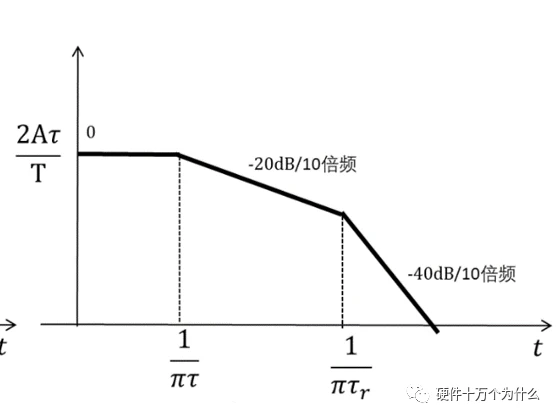
图 14.8方波脉冲和梯形波的单边谱边界
版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/jszy-jszl/47927.html
