一 概述
简单来说,混沌科学中,同一个动力学方程或者是方程组,给出的初始值相差甚微,长时间后,系统的运动轨迹却有很大差别;混沌系统广泛应用在加密等领域。
二 Matlab仿真混沌系统
以chen混沌系统为例:
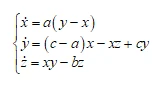
式中x,y,z
是系统的状态变量,a,b,c为该系统的常数,当参数a=35,b=3,c=28时,系统处于混沌状态。用
MATLAB
仿真得到
得到
Chen
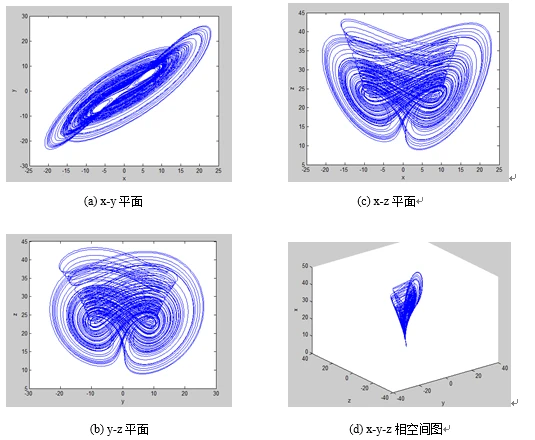
混沌吸引子在
x-y
相面、
x-z
相面、
y-z
相面以及
x-y-z
相空间中的相轨图,如图所示
定义equation.m文件定义chen混沌方程函数
function dy=total(t,y) %%chen circuit a=35;b=3;c=28; dy=[a*(y(2)-y(1)); (c-a)*y(1)-y(1)*y(3)+c*y(2); y(1)*y(2)-b*y(3)]; end
调用实现(matlab中一般使用ODE45函数求解微分方程):
x0=[-1;-0.2;0.5]; tspan=[0:0.001:80]; [T,X]=ode45('equation',tspan,x0); figure(1); subplot(3,1,1),plot(T,X(:,1),'r'); xlabel('t'); ylabel('x'); subplot(3,1,2),plot(T,X(:,2),'r'); xlabel('t'); ylabel('y'); subplot(3,1,3),plot(T,X(:,3),'r'); xlabel('t'); ylabel('z'); figure(2); plot(X(30000:end,1),X(30000:end,2));%grid; xlabel(' x'); ylabel(' y'); figure(3); plot(X(30000:end,1),X(30000:end,3));%grid; xlabel(' x'); ylabel(' z'); figure(4); plot(X(30000:end,2),X(30000:end,3));%grid; xlabel(' y'); ylabel(' z'); figure(5); plot3(X(30000:end,1),X(30000:end,2),X(30000:end,3));%grid; xlabel(' y'); ylabel(' z');%%%%%%%%%%%%%%%%%%%%%%版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/matlabbc/1631.html
