
K平均算法 —— 用于将给定点分成K个聚类(K为事先设定)
K平均算法的目标是找到一个聚类方案,使得它包含k个聚类,且各个聚类的点到其中心的平均距离尽可能小。
我们并不关心是否能够找到一种分割方案使得这个损失函数取到最小值。
我们只需要找到一个分割方案使这个损失函数尽可能小,最后得到的聚类比较合理就可以。
K平均算法的具体步骤如下:
(1)随机选取K个中心作为初始值。
(2)对于数据集中的每个点,分别找到离它最近的中心点,将其归为相应的聚类。
(3)根据已有聚类的分配方案,对每个聚类(包括中心点和数据点),重新计算最优的中心点的位置。具体来说,最优中心点的位置应该是该聚类所有数据点的平均位置。
(4)重复第2步和第3步,直到算法收敛,即中心点的位置与聚类的分配方案不再改变。
核心算法代码:
import numpy as np
# 1. 随机选取K个中心作为初始值# 从数据集X中随机选择k个不同的数据点作为初始中心点def initialize_centroids(X, k): indices = np.random.choice(len(X), k, replace=False) return X[indices]
# 2. 对于数据集中的每个点,分别找到离它最近的中心点,将其归为相应的聚类# 计算数据集中每个点到每个中心点的欧氏距离,并返回每个点最近的中心点的索引def assign_clusters(X, centroids): # 计算每个点与每个中心点的距离 distances = np.sqrt((X - centroids[:, np.newaxis])2).sum(axis=2) # 返回每个点最近的中心点索引 return np.argmin(distances, axis=0)
# 3. 根据已有聚类的分配方案,对每个聚类(包括中心点和数据点),重新计算最优的中心点的位置# 根据当前的聚类结果,重新计算每个聚类中心点的位置,即聚类中所有点的平均位置def update_centroids(X, labels, k): # 对每个聚类计算新的中心点 new_centroids = np.array([X[labels == i].mean(axis=0) for i in range(k)]) return new_centroids
# 4. 重复第2步和第3步,直到算法收敛,即中心点的位置与聚类的分配方案不再改变# K-means算法主函数,执行K-means聚类def kmeans(X, k, max_iters=100): # 初始化中心点 centroids = initialize_centroids(X, k) for i in range(max_iters): # 将每个点分配给最近的中心点 labels = assign_clusters(X, centroids) # 计算新的中心点 new_centroids = update_centroids(X, labels, k) # 如果中心点没有变化,说明已经收敛 if np.all(centroids == new_centroids): break centroids = new_centroids return centroids, labels
# 生成随机点np.random.seed(0)X = np.random.rand(40, 2)
# 执行K-means算法k = 4 # 用户可以修改k的值,表示聚类的数量centroids, labels = kmeans(X, k)算法部分解释:
initialize_centroids 函数从数据集中随机选择 k 个不同的数据点作为初始中心点。
assign_clusters 函数计算数据集中的每个点到每个中心点的欧氏距离,并为每个点分配一个标签,标签是其最近中心点的索引。
update_centroids 函数根据当前的聚类结果重新计算每个聚类的中心点位置。
kmeans 函数是算法的主入口,它初始化中心点,然后在每次迭代中分配聚类并更新中心点,直到满足收敛条件。
最终函数返回聚类中心点 centroids 和每个点的聚类标签 labels。
算法演示视频:
设定随机生成400个点,分割成4个聚类(k=4):
算法其他情况演示:
为了更好地展示效果,我设定为初始随机生成n个点(可修改),分割成k个聚类(可修改),每5秒迭代一次并生成图。
import numpy as npimport matplotlib.pyplot as pltimport time
# 1. 随机选取K个中心作为初始值def initialize_centroids(X, k): indices = np.random.choice(len(X), k, replace=False) return X[indices]
# 2. 对于数据集中的每个点,分别找到离它最近的中心点,将其归为相应的聚类def assign_clusters(X, centroids): distances = np.sqrt(((X - centroids[:, np.newaxis])2).sum(axis=2)) return np.argmin(distances, axis=0)
# 3. 根据已有聚类的分配方案,对每个聚类(包括中心点和数据点),重新计算最优的中心点的位置def update_centroids(X, labels, k): return np.array([X[labels == i].mean(axis=0) for i in range(k)])
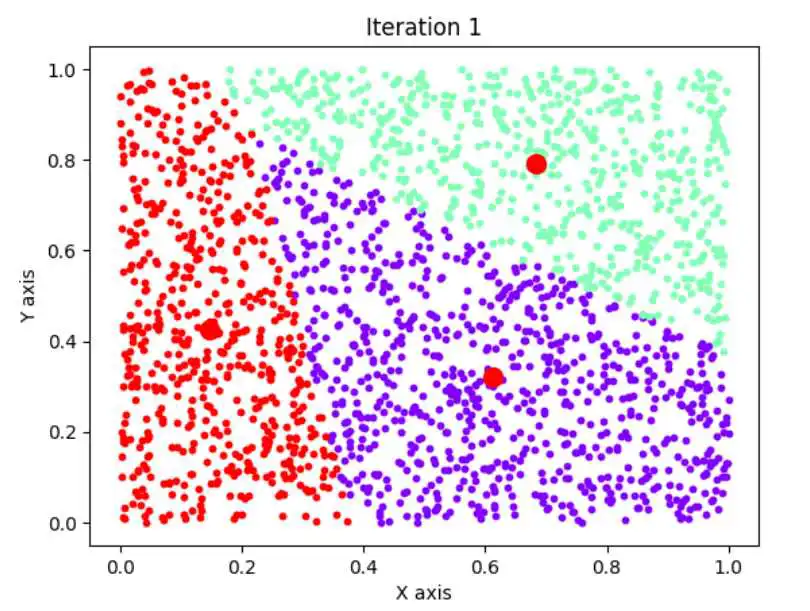
# 4. 重复第2步和第3步,直到算法收敛,即中心点的位置与聚类的分配方案不再改变def kmeans(X, k, max_iters=100): centroids = initialize_centroids(X, k) for i in range(max_iters): labels = assign_clusters(X, centroids) new_centroids = update_centroids(X, labels, k) if np.all(centroids == new_centroids): break centroids = new_centroids plt.clf() # 清除当前图像 colors = ['r', 'b', 'y', 'g'] for j in range(k): plt.scatter(X[labels == j, 0], X[labels == j, 1], s=10, c=colors[j]) plt.scatter(centroids[:, 0], centroids[:, 1], s=100, c='red', marker='o') plt.title(f'Iteration {i+1}') plt.xlabel('X axis') plt.ylabel('Y axis') plt.pause(5) # 每5秒更新一次图像 return centroids, labels
# 生成随机点np.random.seed(0)X = np.random.rand(40, 2)
# 执行K-means算法k = 4 # 用户可以修改k的值centroids, labels = kmeans(X, k)
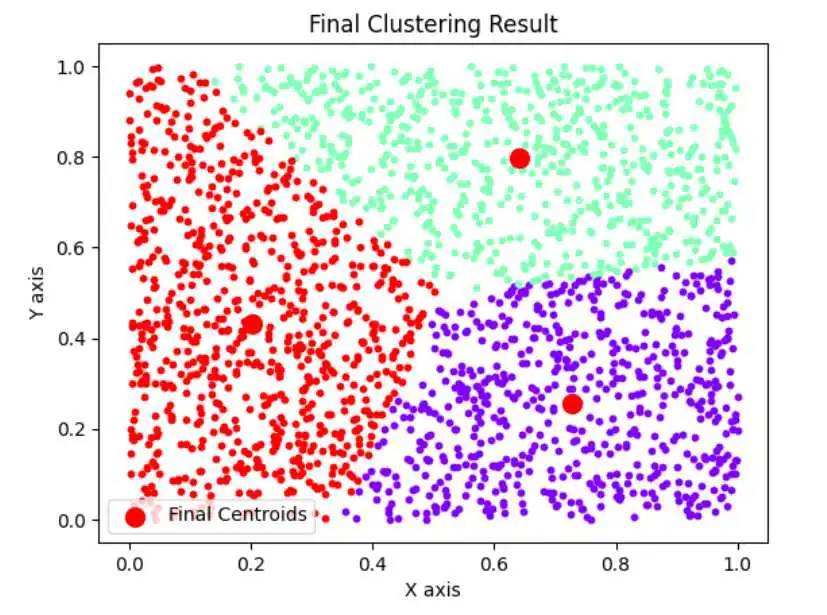
# 绘制最终的聚类结果colors = ['r', 'b', 'y', 'g']for j in range(k): plt.scatter(X[labels == j, 0], X[labels == j, 1], s=10, c=colors[j])plt.scatter(centroids[:, 0], centroids[:, 1], s=100, c='red', marker='o', label='Final Centroids')plt.title('Final Clustering Result')plt.xlabel('X axis')plt.ylabel('Y axis')plt.legend()plt.show()运行结果演示:
红色粗心表示选取的中心点位置。
n=40,k=4
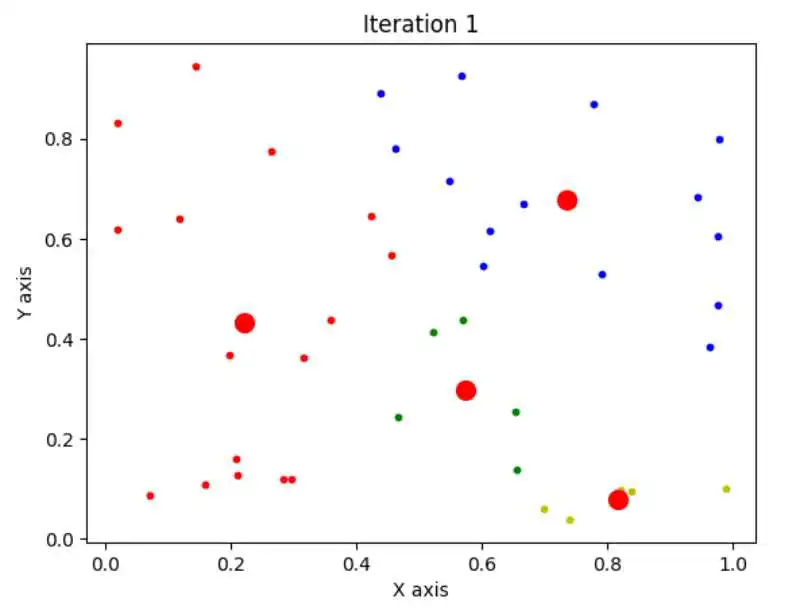
使用K平均算法的最终聚类结果:
上面的这个算法演示我们使用的是40个点,取k=4,大家可能会觉得效果不太明显,如果我们使用1000个点呢?
效果那就会相当明显了,n=1000,k=4,如下图:
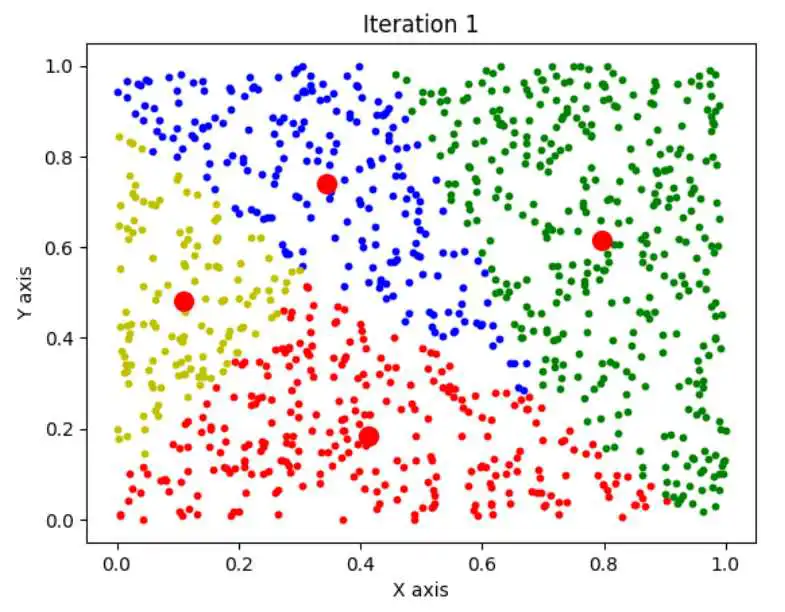
使用K平均算法的最终聚类结果:

上面的代码k最高只能设置成4,我对代码进行优化之后,k可以取任意值。
import numpy as npimport matplotlib.pyplot as pltimport matplotlib.cm as cmimport time
# 1. 随机选取K个中心作为初始值def initialize_centroids(X, k): num_points = len(X) # 确保 k 不大于数据点的数量 k = min(k, num_points) indices = np.random.choice(num_points, k, replace=False) return X[indices]
# 2. 对于数据集中的每个点,分别找到离它最近的中心点,将其归为相应的聚类def assign_clusters(X, centroids): distances = np.sqrt(((X - centroids[:, np.newaxis])2).sum(axis=2)) return np.argmin(distances, axis=0)
# 3. 根据已有聚类的分配方案,对每个聚类(包括中心点和数据点),重新计算最优的中心点的位置def update_centroids(X, labels, k): return np.array([X[labels == i].mean(axis=0) for i in range(k)])
# 4. 重复第2步和第3步,直到算法收敛,即中心点的位置与聚类的分配方案不再改变def kmeans(X, k, max_iters=100): centroids = initialize_centroids(X, k) for i in range(max_iters): labels = assign_clusters(X, centroids) new_centroids = update_centroids(X, labels, k) if np.all(centroids == new_centroids): break centroids = new_centroids plt.clf() # 清除当前图像 colors = cm.rainbow(np.linspace(0, 1, k)) # 生成k个颜色 for j in range(k): plt.scatter(X[labels == j, 0], X[labels == j, 1], s=10, c=colors[j]) plt.scatter(centroids[:, 0], centroids[:, 1], s=100, c='red', marker='o') plt.title(f'Iteration {i+1}') plt.xlabel('X axis') plt.ylabel('Y axis') plt.pause(5) # 每5秒更新一次图像 return centroids, labels
# 生成随机点np.random.seed(0)X = np.random.rand(10000, 2)
# 执行K-means算法k = 9 # 用户可以修改k的值centroids, labels = kmeans(X, k)
# 绘制最终的聚类结果colors = cm.rainbow(np.linspace(0, 1, k)) # 生成k个颜色for j in range(k): plt.scatter(X[labels == j, 0], X[labels == j, 1], s=10, c=colors[j])plt.scatter(centroids[:, 0], centroids[:, 1], s=100, c='red', marker='o', label='Final Centroids')plt.title('Final Clustering Result')plt.xlabel('X axis')plt.ylabel('Y axis')plt.legend()plt.show()下面我们继续对代码进行测试:
n=10000,k=9
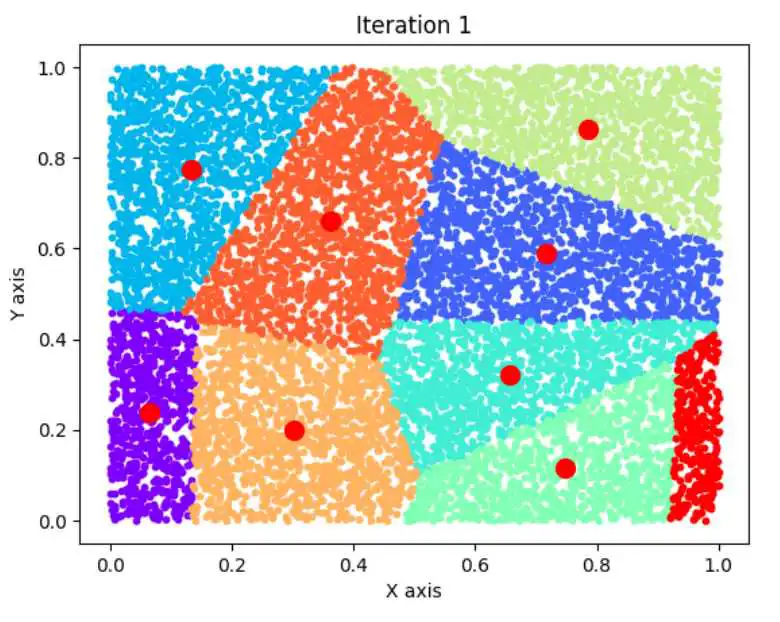
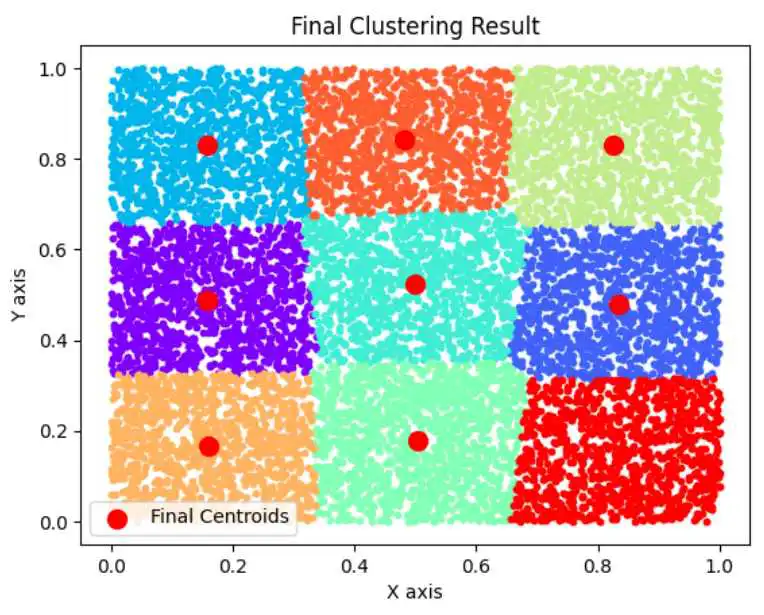
n=10000,k=4
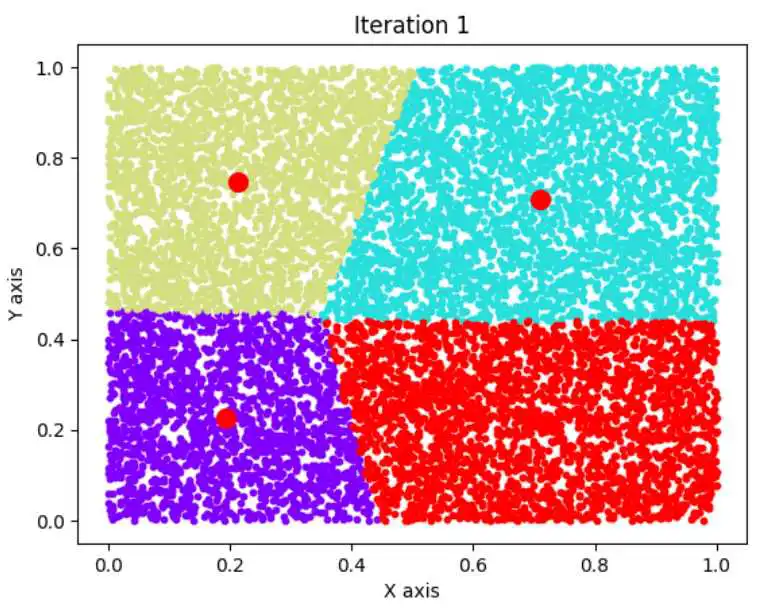

n=5000,k=16

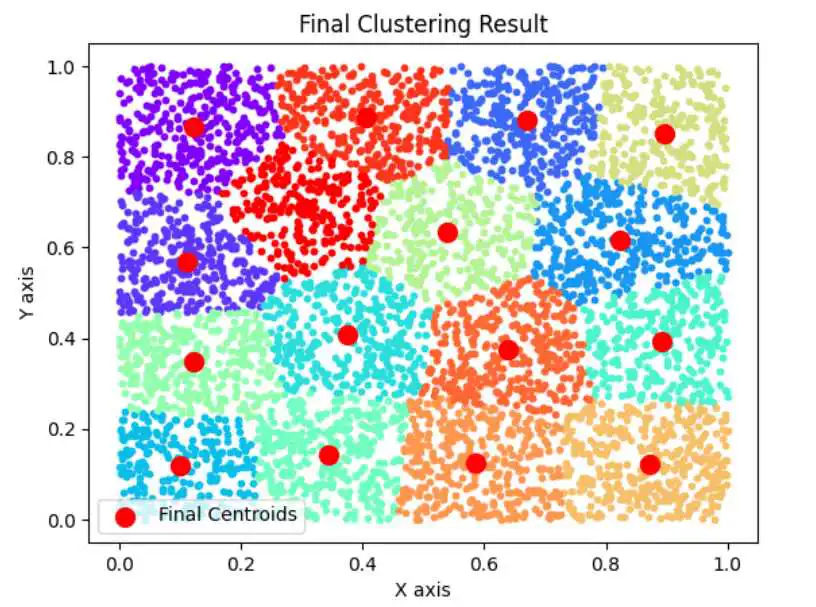
n=2000,k=2
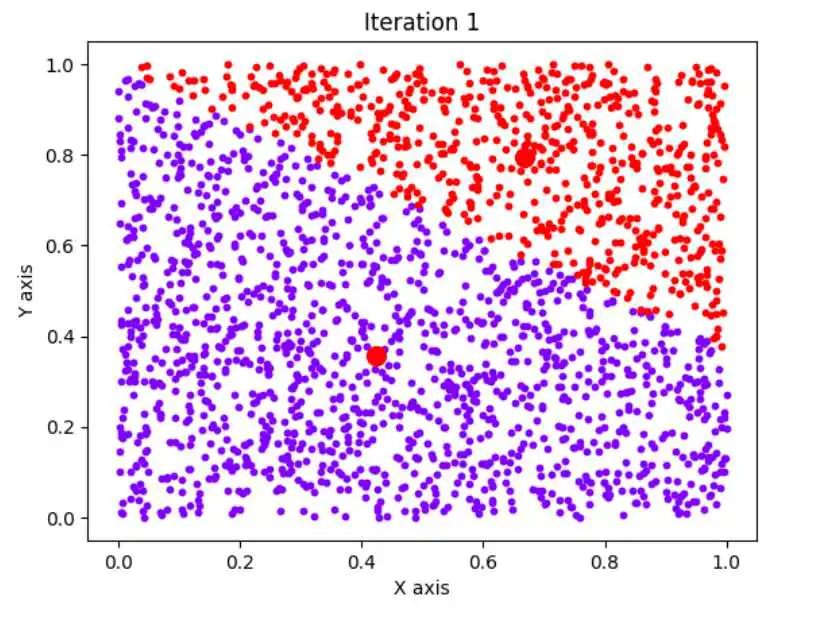
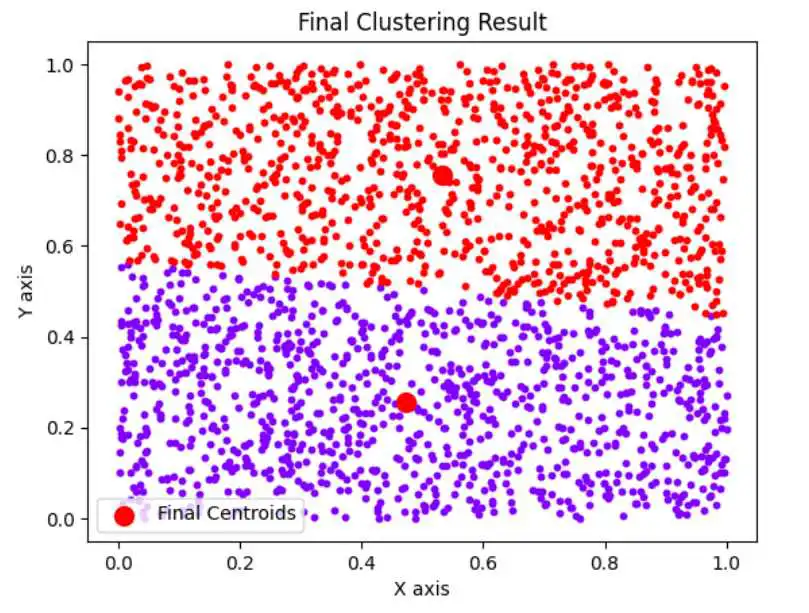
n=2000,k=3
本栏目会持续更新,其中“算法演示”和“问题讨论部分”为完全免费,其他有部分免费,敬请关注更新。
看到这里,相信你也一定发现了一些规律!是不是很有趣!不过这些规律我自己也没有搞明白,挖个坑,等我考完研再来研究一下,倒时候研究结果还是放在这个合集里。
关注公众号后台回复“人工智能”,即可获得姚期智《人工智能》教材。
版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/rfx/19075.html
