提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
使用 文件> 导入数据 > CSV 文件进行导入,在变量示图中保证输入的数据均为并设置对应的数据类型(目前参考数据的y与x均已给定,所有数据均设置为标量型数据)


在SPSS中,选择分析>回归 >线性 进行回归拟合,并在”保存”中选择:未标准化残差和学生化残差,


使用学生化残差构造散点图
观察残差是否随着x的波动有扩大或缩小的趋势,如果有说明存在异方差。(该样本显示随着x2增大,残差有扩大趋势,说明存在残差存在异方差)

a)构造为标准化残差的绝对值:在SPSS中,选择转换>计算变量>目标变量:ABSE,数字表达式:ABS(RES_1) 点击确定。


b)计算等级相关系数:在SPSS中,选择分析>相关>双变量,在变量中选择x1,x2,ABSE,相关系数选择“斯皮尔曼“,


结果显示 相关系数rs为0.721,n=15,计算t值得5.414
给定显著性水平α=0.05,自由度n-2=15-2=13,临界值t0.025(13)=2.160
由于|t|=5.414>2.160,说明残差的绝对值与自变量x2显著相关,存在异方差性。
图中也标明相关性显著

a)首先确认幂底数 :选择幂底数的方法是采用等级相关系数最大的变量为幂底数,参考上面内容可知,x2比x1大,故选择x2为幂底数。

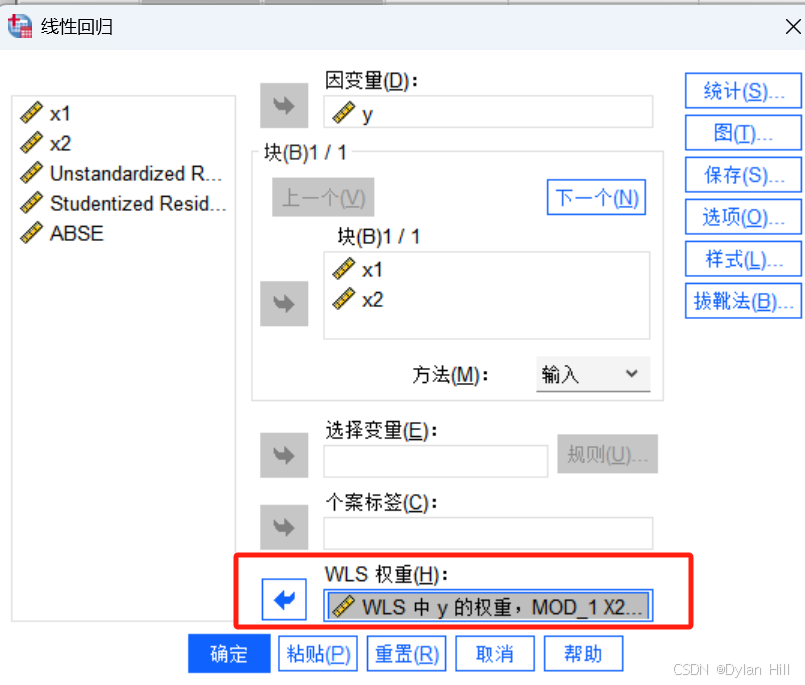
b)其次确认权重w :在SPSS中,选择分析>回归 >权重估算,因变量选择:y,自变量选择:x1,x2;权重变量:x2,功效范文选择[-2,5],步长为0.5;选择“选项“中保留权重为最新变量。
M从 -2到4 的m的最优值为2.5,输出结果如下图3所示。



进行加权最小二乘法建模:选择分析>回归 >线性,在”WLS权重”中将保留的权重进行选择,点击确定保存,针对加权后的残差进一步观测加权的残差图,观测是否存在异方差。


观察并分析最小二乘法的回归模型
对比普通最小二乘法和加权二乘法的系数、模型拟合以及方差分析表判断最小二乘法拟合效果
普通最小:

加权最小:

导入数据
在SPSS中,使用 文件> 导入数据 > CSV 文件进行导入,在变量示图中保证输入的数据均为并设置对应的数据类型

在SPSS中,选择 分析> 回归 > 线性,在保存中计算“未标准化残差“ ,选择图形>旧对话框 > 散点图画出未标准化残差的散点图,观察散点图随着x波动前后呈现锯齿状或者循环变化的情况,如果存在说明方差前后自相关(观察残差图发现残差呈现循环变化,所以残差存在自相关)。


在SPSS中,选择分析>回归> 线性,在线性回归的框架下在“统计(S)“下选择”德滨-沃森“
DW=0.745 查DW表dl=1.50
由DW=0.745<1.50,可知残差存在正的自相关,
自相关系数p=1-0.5DW=0.6275 说明误差项存在自相关


a)用首先要进行自相关系数p,p=1-0.5DW,DW由以上可知为0.745

b)构造中间变量:首先复制一份y、x1、x2,并将第2-n行数据粘贴在1-n-1行,主要构造y的前后变量,中间变量:y_1、x1_1、x2_1

c)变量转化:变量转化,y’t=yt-p*yt-1



d)用新变量做线性回归:观测新变量的的残差及dw值,是否存在自相关情况。,计算DW=1.716 查DW表,d₁<dw=1.716<4- du,可知残差落入无自相关区域。


e)构造新的回归方程:由新变量输出的参数值构造的参数方程如下
y_2=211.110x1_2 + 1.437x2_2 -178.845
(特殊注意,需要还原到原来变量的方程)
将y_2=y_1-0.6275y x1_2=x1_1-0.6275x1 x2_2=x2_1-0.6275x2代入,还原为原始变量的方程

a)用差分法解决自相关问题与迭代法的区别是,将p=1,用新的p来构造新的变量
构建中间变量同上,变量转化时用p=1来构造新变量

b)用新变量做线性回归(查分法需要剔除常量):观测新变量的的残差及dw值,是否存在自相关情况。


查DW表,得dl<DW=2.040<4-du.可知残差落入无自相关区域。
误差项的标准差也从原先的329.69302降到了现在的280.98995

c)构造新的回归方程:由新变量输出的参数值构造的参数方程如下
由下表知新变量的 β1=210.117 β2=1.397
y_3=210.117x1_3 + 1.397x2_3
将y_3=y_1-y x1_3=x1_1-x1 x2_3=x2_1-x2代入,还原为原始变量的方程(y_3为新变量,y_1为中间变量,y为原始变量)

在SPSS中,使用 分析> 回归> 线性->保存 中选择未标准化、学生化、删除学生化、库克距离、杠杆值后点击继续进而确定。

通过下图显示:绝对值最大的学生化残差为SRE₁₅=2.613,小于3,因而根据学生化残差诊断认为数据不存在异常值。绝对值最大的删除学生化残差为SRE(15)=3.810, 因而根据删除学生化残差诊断认为第15个数据为异常值。其中心化杠杆值ch;=0.339库克距离D,=1.555由于第15个数据ch,=0.339>2ch, 因而从杠杆值看,第15个数据是自变量的异常值, 同时库克距离D₁₅=1.555>1, 这样第15个数据为异常值是由自变量异常与因变量异常两个原因共同引起的。诊断出异常值后,进一步要判断产生异常值的原因。产生异常值的原因通常有几个:数据登记误差、测量误差、随机误差、缺少重要自变量、存在异方差、模型选用错误等原因。

加权后的删除学生化残差、杠杆值,库克距离如下,目前观测数据没有异常值


版权声明:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若内容造成侵权、违法违规、事实不符,请将相关资料发送至xkadmin@xkablog.com进行投诉反馈,一经查实,立即处理!
转载请注明出处,原文链接:https://www.xkablog.com/sjkxydsj/73504.html
